题目内容
12．
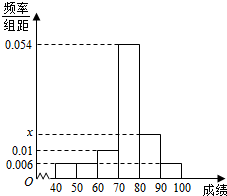某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]．已知图中x=0.018，则由直观图估算出中位数（精确到0.1）的值为（ ）| A． | 75.5 | B． | 75.2 | C． | 75.1 | D． | 75.3 |
分析 根据频率分布直方图，利用中位数两侧的频率相等，列出方程求出中位数的值．
解答 解：根据频率分布直方图，得；
（0.006×2+0.01）×10=0.22＜0.5，
0.22+0.054×10=0.76＞0.5，
所以中位数应在[70，80）内，可设为x，
则（x-70）×0.054+0.22=0.5，
解得x≈75.2．
故选：B．
点评 本题考查了利用频率分布直方图求中位数的应用问题，解题时要熟练掌握直方图的基本性质，是基础题．
练习册系列答案
相关题目
2．在△ABC中，角A，B，C的对边是a，b，c，若asinA=csinC，b2+ac=a2+c2，则a，b，c等于（ ）
| A． | 1：1：2 | B． | 1：$\sqrt{2}$：1 | C． | 1：1：1 | D． | 1：1：$\sqrt{2}$ |
3．设α、β为不重合的平面，m，n为不重合的直线，则下列命题正确的是（ ）
| A． | 若m∥α，n∥β，m⊥n，则α⊥β | B． | 若m∥n，n∥α，α∥β，则m∥β | ||
| C． | 若α⊥β，α∩β=n，m⊥n，则m⊥α | D． | 若α∩β=n，m∥α，m∥β，则m∥n |
20．过点（0，2b）的直线l与双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）的一条斜率为正值的渐近线平行，若双曲线C的右支上的点到直线l的距离恒大于b，则双曲线C的离心率的取值范围是（ ）
| A． | （1，2] | B． | （2，+∞） | C． | （1，2） | D． | （1，$\sqrt{2}$] |
17．“$\frac{1}{x}$＜3”是“x＞$\frac{1}{3}$”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
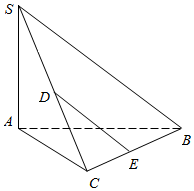如图，在三棱锥S-ABC中，SA⊥底面ABC，BC⊥AC，D、E分别是SC、BC的中点．