题目内容
15.已知Rt△ABC三个顶点的坐标分别为A(t,0),B(1,2),C(0,3),则实数t的值为-1或-3.分析 由题意画出图形,分类利用向量数量积为0求得实数t的值.
解答 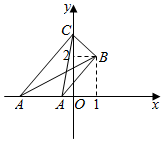 解:如图,
解:如图,
由图可知,角B或角C为直角.
当B为直角时,$\overrightarrow{BC}=(-1,1)$,$\overrightarrow{BA}=(t-1,-2)$,由$\overrightarrow{BA}•\overrightarrow{BC}=0$得,-(t-1)-2=0,即t=-1;
当C为直角时,$\overrightarrow{CB}=(1,-1),\overrightarrow{CA}=(t,-3)$,由$\overrightarrow{CB}•\overrightarrow{CA}=0$得,t+3=0,即t=-3.
故答案为:-1或-3.
点评 本题考查两直线垂直的关系,考查了向量数量积判断两直线的垂直,体现了分类讨论的数学思想方法,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.一个长方体的底面是边长为2的正方形,高为$\sqrt{2}$,其俯视图是面积为4的正方形,侧视图是一个面积为4的矩形,则该长方体正视图的面积为( )
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 8 | D. | 4$\sqrt{2}$ |
3.设α、β为不重合的平面,m,n为不重合的直线,则下列命题正确的是( )
| A. | 若m∥α,n∥β,m⊥n,则α⊥β | B. | 若m∥n,n∥α,α∥β,则m∥β | ||
| C. | 若α⊥β,α∩β=n,m⊥n,则m⊥α | D. | 若α∩β=n,m∥α,m∥β,则m∥n |
20.过点(0,2b)的直线l与双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的一条斜率为正值的渐近线平行,若双曲线C的右支上的点到直线l的距离恒大于b,则双曲线C的离心率的取值范围是( )
| A. | (1,2] | B. | (2,+∞) | C. | (1,2) | D. | (1,$\sqrt{2}$] |
5.已知全集U=R,集合A={x|($\frac{1}{2}$)x≤1,B={x|x2-6x+8≤0},则A∩B为( )
| A. | {x|x≤0} | B. | {x|2≤x≤4} | C. | {x|0<x≤2或x≥4} | D. | {x|0≤x<2或x>4} |
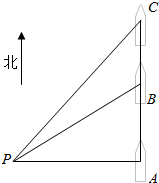 已知在观测点P处测得在正东方向A处一轮船正在沿正北方向匀速航行,经过1小时后在观测点P测得轮船位于北偏东60°方向B处,又经过t小时发现该轮船在北偏东45°方向C处,则t=$\sqrt{3}-1$.
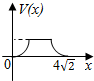
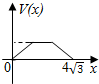
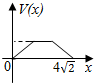
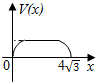
已知在观测点P处测得在正东方向A处一轮船正在沿正北方向匀速航行,经过1小时后在观测点P测得轮船位于北偏东60°方向B处,又经过t小时发现该轮船在北偏东45°方向C处,则t=$\sqrt{3}-1$.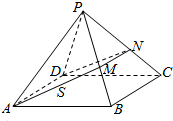 在四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S-ABCD的体积为V(x),则函数V(x)的图象是( )
在四棱锥P-ABCD中,各侧面是全等的等腰三角形,腰长为4且顶角为30°,底面是正方形(如图),在棱PB,PC上各有一点M、N,且四边形AMND的周长最小,点S从A出发依次沿四边形AM,MN,ND运动至点D,记点S行进的路程为x,棱锥S-ABCD的体积为V(x),则函数V(x)的图象是( )