题目内容
13.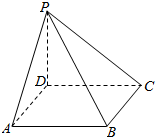 已知线段PD垂直于正方形ABCD所在平面,D为垂足,|PD|=5cm,|AB|=8cm,连接PA、PB、PC.
已知线段PD垂直于正方形ABCD所在平面,D为垂足,|PD|=5cm,|AB|=8cm,连接PA、PB、PC.(1)求证:平面PBC⊥平面PDC;
(2)求PB与平面ABCD所成角的正切值.
分析 (1)证明PD⊥BC,BC⊥CD,可得BC⊥平面PDC,即可证明平面PBC⊥平面PDC;
(2)确定∠PBD是PB与平面ABCD所成角,即可求PB与平面ABCD所成角的正切值.
解答  证明:(1)因为PD⊥面ABCD,所以PD⊥BC.
证明:(1)因为PD⊥面ABCD,所以PD⊥BC.
因为ABCD是正方形,所以BC⊥CD,
因为PD∩CD=D
所以BC⊥平面PDC,
又BC⊆平面PBC,所以平面PBC⊥平面PDC.…(3分)
(2)因为PD⊥面ABCD,所以BD为PB在面ABCD内射影,
即∠PBD是PB与平面ABCD所成角.…(5分)
在Rt△PDB中,|PD|=5cm,$|{BD}|=8\sqrt{2}$cm,所以tan∠PBD=$\frac{{|{PD}|}}{{|{BD}|}}=\frac{{5\sqrt{2}}}{16}$.…(7分)
点评 本题考查线面垂直,平面与平面垂直,考查线面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
3.设α、β为不重合的平面,m,n为不重合的直线,则下列命题正确的是( )
| A. | 若m∥α,n∥β,m⊥n,则α⊥β | B. | 若m∥n,n∥α,α∥β,则m∥β | ||
| C. | 若α⊥β,α∩β=n,m⊥n,则m⊥α | D. | 若α∩β=n,m∥α,m∥β,则m∥n |
5.已知全集U=R,集合A={x|($\frac{1}{2}$)x≤1,B={x|x2-6x+8≤0},则A∩B为( )
| A. | {x|x≤0} | B. | {x|2≤x≤4} | C. | {x|0<x≤2或x≥4} | D. | {x|0≤x<2或x>4} |
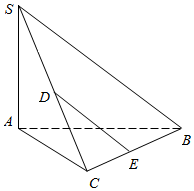 如图,在三棱锥S-ABC中,SA⊥底面ABC,BC⊥AC,D、E分别是SC、BC的中点.
如图,在三棱锥S-ABC中,SA⊥底面ABC,BC⊥AC,D、E分别是SC、BC的中点.