题目内容
已知函数f(x)=ax2-1nx,x∈(0,e],其中e是自然对数的底数,a∈R.
(1)当a=1时,求函数f(x)的单调区间与极值;
(2)对于任意的x∈(0,e],f(x)≥3恒成立,求实数a的取值范围.
(1)当a=1时,求函数f(x)的单调区间与极值;
(2)对于任意的x∈(0,e],f(x)≥3恒成立,求实数a的取值范围.
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(1)求导数,分类讨论,利用导数的正负,可得函数f(x)的单调区间与极值;
(2)对于任意的x∈(0,e],f(x)≥3恒成立,等价于f(x)min≥3,分类讨论,求最值,即可求实数a的取值范围.
(2)对于任意的x∈(0,e],f(x)≥3恒成立,等价于f(x)min≥3,分类讨论,求最值,即可求实数a的取值范围.
解答:
解:(1)当a=1时,f′(x)=
,
x∈(0,
)时,f(x)单调递减,x∈(
,e)时,f(x)单调递增,
所以x=
时,f(x)极小值=f(
)=
+
ln2;
(2)任意的x∈(0,e],f(x)≥3恒成立,等价于f(x)min≥3,
f′(x)=
,x∈(0,e],
①a≤0时,f′(x)<0,f(x)在(0,e)递减,f(x)min=f(e)=ae2-1≥3,∴a≥
,不符合题意;
②a>0时,f′(x)=
=0,得x=±
.
若
≥e,即a≤
,则f'(x)≤0,f(x)在(0,e]递减,fmin(x)=f(e)所以f(e)=ae2-1≥3⇒a≥
,所以a无解. (12分)
若
<e,即a>
时,当x∈(0,
)时f(x)单调递减;当x∈(
,e)时f(x)单调递增.
所以fmin(x)=f(
)=
+
ln2a,
+
ln2a≥3,解得a≥
,
所以a≥
(15分)
| 2x2-1 |
| x |
x∈(0,
| ||
| 2 |
| ||
| 2 |
所以x=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)任意的x∈(0,e],f(x)≥3恒成立,等价于f(x)min≥3,
f′(x)=
| 2ax2-1 |
| x |
①a≤0时,f′(x)<0,f(x)在(0,e)递减,f(x)min=f(e)=ae2-1≥3,∴a≥
| 4 |
| e2 |
②a>0时,f′(x)=
| 2ax2-1 |
| x |
|
若
|
| 1 |
| 2e2 |
| 4 |
| e2 |
若
|
| 1 |
| 2e2 |
|
|
所以fmin(x)=f(
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| e5 |
| 2 |
所以a≥
| e5 |
| 2 |
点评:本题考查利用导数研究函数的单调性、求函数在闭区间上的最值及恒成立问题,考查转化思想、分类讨论思想,考查学生分析解决问题的能力,属中档题.

练习册系列答案
相关题目
在梯形ABCD中,AB∥DC,AD⊥AB,AB=2AD=2DC=4,点N是CD边上一动点,则
•
的最大值为( )
| AN |
| AB |
A、4
| ||
| B、8 | ||
C、8
| ||
| D、16 |
函数y=x3-3x+1在[-2,1]上的最大值为( )
| A、3 | B、4 | C、5 | D、6 |
某次中俄军演中,中方参加演习的有4艘军舰、3架飞机;俄方有5艘军舰、2架飞机.从中俄两方中各选出2个单位(1艘军舰或1架飞机都作为一个单位,所有的军舰两两不同,所有的飞机两两不同),则选出的四个单位中恰有一架飞机的不同选法共有( )
| A、180种 | B、160种 |
| C、120种 | D、38种 |
对于定义在R上的奇函数f(x),满足f(x+3)=f(x),则f(1)+f(2)+f(3)=( )
| A、0 | B、-1 | C、3 | D、2 |
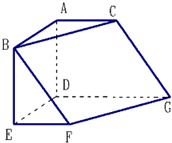 在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形 ABED 是矩形,四边形ADGC 是直角梯形,∠ADG=90°,四边形 DEFG 是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.
在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形 ABED 是矩形,四边形ADGC 是直角梯形,∠ADG=90°,四边形 DEFG 是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.