题目内容
设数列{an}的前n项和为Sn,a1=1,Sn=2an-1.
(1)求{an}的通项an;
(2)求数列{nan}的前n项和为Tn,求使Tn>8n-7的最小正整数n.
(1)求{an}的通项an;
(2)求数列{nan}的前n项和为Tn,求使Tn>8n-7的最小正整数n.
考点:数列的求和,数列的函数特性
专题:等差数列与等比数列
分析:(1)当n≥2时,利用an=Sn-Sn-1可得an=2an-1,利用等比数列的通项公式即可得出.
(2)nan=n•2n-1.利用“错位相减法”可得数列{nan}的前n项和为Tn,进而得出.
(2)nan=n•2n-1.利用“错位相减法”可得数列{nan}的前n项和为Tn,进而得出.
解答:
解:(1)当n≥2时,an=Sn-Sn-1=2an-1-(2an-1-1),化为an=2an-1,
∴数列{an}是等比数列,通项an=1×2n-1.
(2)∵nan=n•2n-1.
∴数列{nan}的前n项和为Tn=1+2×2+3×22+…+n•2n-1,
∴2Tn=2+2×22+…+(n-1)•2n-1+n•2n,
两式相减可得:-Tn=1+2+22+…+2n-1-n•2n=
-n•2n=(1-n)•2n-1,
∴Tn=(n-1)•2n+1.
Tn>8n-7化为(n-1)•2n+8>8n,
化为(n-1)(2n-8)>0,
n=1,2,3时都不成立.
当n=4时成立,
∴使Tn>8n-7的最小正整数n=4.
∴数列{an}是等比数列,通项an=1×2n-1.
(2)∵nan=n•2n-1.
∴数列{nan}的前n项和为Tn=1+2×2+3×22+…+n•2n-1,
∴2Tn=2+2×22+…+(n-1)•2n-1+n•2n,
两式相减可得:-Tn=1+2+22+…+2n-1-n•2n=
| 2n-1 |
| 2-1 |
∴Tn=(n-1)•2n+1.
Tn>8n-7化为(n-1)•2n+8>8n,
化为(n-1)(2n-8)>0,
n=1,2,3时都不成立.
当n=4时成立,
∴使Tn>8n-7的最小正整数n=4.
点评:本题考查了递推式的意义、等比数列的通项公式及其前n项和公式、“错位相减法”,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
不等式组
所表示的平面区域的面积为( )
|
A、
| ||
| B、27 | ||
| C、30 | ||
D、
|
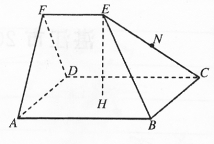 如图,五面体EF-ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面 ABCD,AB=2,EF=EH=1.
如图,五面体EF-ABCD中,ABCD是以点H为中心的正方形,EF∥AB,EH丄平面 ABCD,AB=2,EF=EH=1.
