题目内容
已知x>-1,则函数y=x+
的最小值为( )
| 1 |
| x+1 |
| A、-1 | B、0 | C、1 | D、2 |
考点:基本不等式在最值问题中的应用
专题:计算题,不等式的解法及应用
分析:y=x+
=x+1+
-1,利用基本不等式求最值.
| 1 |
| x+1 |
| 1 |
| x+1 |
解答:
解:y=x+
=x+1+
-1≥2
-1=2-1=1(当且仅当x+1=
,即x=0时,等号成立).
故选:C.
| 1 |
| x+1 |
| 1 |
| x+1 |
(x+1)•
|
| 1 |
| x+1 |
故选:C.
点评:本题由题意首先化简为y=x+1+
-1的形式,再出基本不等式求解,属于基础题.
| 1 |
| x+1 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
数列{an}的前n项和为Sn,若Sn=3+2an(n∈N*),则这个数列一定是( )
| A、等比数列 |
| B、等差数列 |
| C、从第二项起是等比数列 |
| D、从第二项起是等差数列 |
有穷数列5,8,11,…3n+11(n∈N*)的项数是( )
| A、n | B、3n+11 |
| C、n+4 | D、n+3 |
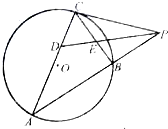 如图,PC是圆O的切线,切点为C,直线PA与圆O交于两点A、B,∠APC的平分线分别交弦CA、CB于两点D、E,已知PC=3,PB=2,则
如图,PC是圆O的切线,切点为C,直线PA与圆O交于两点A、B,∠APC的平分线分别交弦CA、CB于两点D、E,已知PC=3,PB=2,则