题目内容
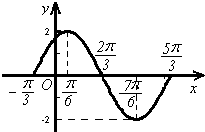
函数y=Asin（ωx+ϕ）在一个周期内的图象如右图所示，此函数的解析式为（ ）
A、y=2sin（x+
| ||||
B、y=2sin（2x+
| ||||
C、y=2sin（
| ||||
D、y=2sin（2x-
|
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：由函数的图象的顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值，可得函数的解析式．
解答：
解：由函数的图象可得A=2，
=
=
-
，∴ω=1．
再根据五点法作图可得 1×（-
）+φ=0，
∴φ=
，
∴函数的解析式为 y=2sin（x+
），
故选：A．
| T |
| 2 |
| π |
| ω |
| 7π |
| 6 |
| π |
| 6 |
再根据五点法作图可得 1×（-
| π |
| 3 |
∴φ=
| π |
| 3 |
∴函数的解析式为 y=2sin（x+
| π |
| 3 |
故选：A．
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，由函数的图象的顶点坐标求出A，
周期求出ω，由五点法作图求出φ的值，属于基础题．
周期求出ω，由五点法作图求出φ的值，属于基础题．
练习册系列答案
相关题目
函数 y=f（x），x∈D，若存在常数C，对任意的x1∈D，存在唯一的x2∈D使得
=C，则称函数f（x）在D上的几何平均数为C．已知f（x）=x3，x∈[1，2]，则函数f（x）=x3在[1，2]上的几何平均数为（ ）
| f(x1)f(x2) |
A、
| ||
| B、2 | ||
| C、4 | ||
D、2
|
下列说法：
①将一组数据中的每一个数据都加上或减去同一个常数后，方差恒不变；
②设有一个回归方程
=3-5x，变量x增加一个单位时，y平均增加5个单位；
③相关系数r越接近1，说明模型的拟和效果越好；
其中错误的个数是（ ）
①将一组数据中的每一个数据都加上或减去同一个常数后，方差恒不变；
②设有一个回归方程
| ∧ |
| y |
③相关系数r越接近1，说明模型的拟和效果越好；
其中错误的个数是（ ）
| A、1 | B、2 | C、3 | D、0 |
下列四组函数中，表示同一函数的是（ ）
A、y=
| |||||
| B、y=1与y=x0 | |||||
| C、y=2x+1与y=2t+1 | |||||
D、y=x与y=(
|
若函数f（x）=
在区间（a，a+
） （a≥0）上有极值，则实数a的取值范围是（ ）
| 1+lnx |
| x |
| 2 |
| 3 |
| A、（0，1） | ||
B、（
| ||
C、（
| ||
D、（
|
已知映射f：M→N，使集合N中的元素y=x2与集合M中的元素x对应，要使映射f：M→N是一一对应，那么M，N可以是（ ）
| A、M=R，N=R |
| B、M=R，N={y|y≥0} |
| C、M={x|x≥0}，N=R |
| D、M={x|x≥0}，N={y|y≥0} |