题目内容
设向量
=(cos25°,sin25°),
=(sin20°,cos20°),若t是实数,且
=
+t
,则|
|的最小值为( )
| a |
| b |
| u |
| a |
| b |
| u |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:求出向量a,b的模和数量积,求出
2=(
+t
)2=
2+t2
2+2t
•
,代入数值,配方求出最小值即可.
| u |
| a |
| b |
| a |
| b |
| a |
| b |
解答:
解:∵向量
=(cos25°,sin25°),
=(sin20°,cos20°),
∴|
|=|
|=1,
•
=cos25°sin20°+sin25°cos20°═sin45°=
.
则
2=(
+t
)2=
2+t2
2+2t
•
=1+t2+
t=(t+
)2+
,
故当t=-
时,
2取最小值
,则|
|的最小值为
.
故选B.
| a |
| b |
∴|
| a |
| b |
| a |
| b |
| ||
| 2 |
则
| u |
| a |
| b |
| a |
| b |
| a |
| b |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
故当t=-
| ||
| 2 |
| u |
| 1 |
| 2 |
| u |
| ||
| 2 |
故选B.
点评:本题考查平面向量的数量积的坐标表示,及性质:向量的平方即为模的平方,考查二次函数的最值,属于基础题.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
{an}是等差数列,Sn是其前n项和,a1-a4-a8+2a6+a15=2,则S15=( )
| A、30 | B、15 |
| C、-30 | D、-15 |
设a=sin
,b=cos
,c=tan
,则( )
| 3π |
| 7 |
| 2π |
| 7 |
| 5π |
| 7 |
| A、b>a>c |
| B、a>b>c |
| C、c>a>b |
| D、b>c>a |
已知f(x)是定义在R上的函数,且满足f(1+x)=f(1-x),则“f(x)为偶函数”是“2为函数f(x)的一个周期”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知函数f(x)=
,则
f(x)dx=( )
|
| ∫ | 2 0 |
| A、4 | ||
| B、3 | ||
| C、2 | ||
D、
|
函数y=Asin(ωx+ϕ)在一个周期内的图象如右图所示,此函数的解析式为( )
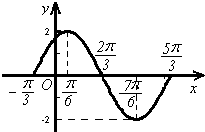

A、y=2sin(x+
| ||||
B、y=2sin(2x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x-
|
双曲线
-
=1(a>0,b>0)与直线y=2x有公共点,则双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||
B、(
| ||
C、(1,
| ||
D、[
|
定义运算:x⊙y=
,如2⊙5=2,则下列等式不能成立的是( )
|
| A、x⊙y=y⊙x |
| B、(x⊙y)⊙z=x⊙(y⊙z) |
| C、(x⊙y)2=x2⊙y2 |
| D、c•(x⊙y)=(c•x)⊙(c•y)(其中c>0) |