题目内容
函数 y=f(x),x∈D,若存在常数C,对任意的x1∈D,存在唯一的x2∈D使得
=C,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为( )
| f(x1)f(x2) |
A、
| ||
| B、2 | ||
| C、4 | ||
D、2
|
考点:进行简单的合情推理
专题:探究型,推理和证明
分析:根据已知中对于函数y=f(x),x∈D,若存在常数C,对任意x1∈D,存在唯一的x2∈D,使得
=C,则称函数f(x)在D上的几何平均数为C.我们易得若函数在区间D上单调递增,则C应该等于函数在区间D上最大值与最小值的几何平均数,由f(x)=x3,D=[1,2],代入即可得到答案.
| f(x1)f(x2) |
解答:
解:根据已知中关于函数f(x)在D上的几何平均数为C的定义,
结合f(x)=x3在区间[1,2]单调递增
则x1=1时,存在唯一的x2=2与之对应
故C=
=2
故选D.
结合f(x)=x3在区间[1,2]单调递增
则x1=1时,存在唯一的x2=2与之对应
故C=
| 1×8 |
| 2 |
故选D.
点评:此题主要考查了应用新定义分析题意解决问题.对于新定义的问题,需要认真分析定义内容,切记不可偏离题目.

练习册系列答案
相关题目
(2+x)2+(2+x)3+(2+x)4的展开式中x2的系数是( )
| A、3 | B、10 | C、24 | D、31 |
{an}是等差数列,Sn是其前n项和,a1-a4-a8+2a6+a15=2,则S15=( )
| A、30 | B、15 |
| C、-30 | D、-15 |
极坐标方程ρ=cosθ化为直角坐标方程为( )
A、(x+
| ||||
B、x2+(y+
| ||||
C、x2+(y-
| ||||
D、(x-
|
设a=sin
,b=cos
,c=tan
,则( )
| 3π |
| 7 |
| 2π |
| 7 |
| 5π |
| 7 |
| A、b>a>c |
| B、a>b>c |
| C、c>a>b |
| D、b>c>a |
已知f(x)是定义在R上的函数,且满足f(1+x)=f(1-x),则“f(x)为偶函数”是“2为函数f(x)的一个周期”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数y=Asin(ωx+ϕ)在一个周期内的图象如右图所示,此函数的解析式为( )
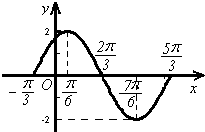

A、y=2sin(x+
| ||||
B、y=2sin(2x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x-
|
点(
,0)到直线x-y=0的距离为( )
| 2 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|