题目内容
若函数f（x）=
在区间（a，a+
） （a≥0）上有极值，则实数a的取值范围是（ ）
| 1+lnx |
| x |
| 2 |
| 3 |
| A、（0，1） | ||
B、（
| ||
C、（
| ||
D、（
|
考点：利用导数研究函数的极值
专题：导数的概念及应用
分析：由已知得f′（x）=
，由f′（x）=0，得x=1，从而
，解得
＜a＜1．
| -lnx |
| x2 |
|
| 1 |
| 3 |
解答：
解：∵函数f（x）=
，
∴f′（x）=
，
由f′（x）=0，得x=1，
∵函数f（x）=
在区间（a，a+
） （a≥0）上有极值，
∴
，解得
＜a＜1．
故选：D．
| 1+lnx |
| x |
∴f′（x）=
| -lnx |
| x2 |
由f′（x）=0，得x=1，
∵函数f（x）=
| 1+lnx |
| x |
| 2 |
| 3 |
∴
|
| 1 |
| 3 |
故选：D．
点评：本题考查实数值的取值范围的求法，是中档题，解题时要认真审题，注意导数性质的合理运用．
练习册系列答案
相关题目
（2+x）2+（2+x）3+（2+x）4的展开式中x2的系数是（ ）
| A、3 | B、10 | C、24 | D、31 |
已知f（x）是定义在R上的函数，且满足f（1+x）=f（1-x），则“f（x）为偶函数”是“2为函数f（x）的一个周期”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
函数y=Asin（ωx+ϕ）在一个周期内的图象如右图所示，此函数的解析式为（ ）
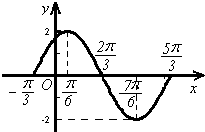
A、y=2sin（x+
| ||||
B、y=2sin（2x+
| ||||
C、y=2sin（
| ||||
D、y=2sin（2x-
|
a，b，c，d均为实数，下列命题正确的个数有（ ）
①a＞b，c＞b⇒a＞c；②a＞-b⇒c-a＜c+b；③a＞b⇒ac2＞bc2； ④a＞b，c＞d⇒ac＞bd；⑤
＞
⇒a＞b．
①a＞b，c＞b⇒a＞c；②a＞-b⇒c-a＜c+b；③a＞b⇒ac2＞bc2； ④a＞b，c＞d⇒ac＞bd；⑤
| a |
| c2 |
| b |
| c2 |
| A、1 | B、2 | C、3 | D、4 |
双曲线
-
=1（a＞0，b＞0）与直线y=2x有公共点，则双曲线的离心率的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、（1，
| ||
B、（
| ||
C、（1，
| ||
D、[
|
以下命题不正确的是（ ）
| A、?x∈N，lgx=2 | ||||
B、双曲线
| ||||
| C、?x∈R，2x-1＞0 | ||||
D、抛物线x=2y2的准线方程为x=-
|
点（
，0）到直线x-y=0的距离为（ ）
| 2 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|