题目内容
若A,B,C为△ABC的三个内角,则
+
的最小值为 .
| 9 |
| A |
| 1 |
| B+C |
考点:基本不等式
专题:导数的综合应用
分析:利用三角形的内角和定理可得
+
=
+
.令f(x)=
+
,(x∈(0,π)).利用导数研究其单调性即可得出.
| 9 |
| A |
| 1 |
| B+C |
| 9 |
| A |
| 1 |
| π-A |
| 9 |
| x |
| 1 |
| π-x |
解答:
解:
+
=
+
.
令f(x)=
+
,(x∈(0,π)).
f′(x)=-
+
=
,
令f′(x)>0,解得
<x<π;令f′(x)<0,解得0<x<
.
当且仅当x=
时,函数f(x)取得最小值,f(
)=
+
=
.
故答案为:
.
| 9 |
| A |
| 1 |
| B+C |
| 9 |
| A |
| 1 |
| π-A |
令f(x)=
| 9 |
| x |
| 1 |
| π-x |
f′(x)=-
| 9 |
| x2 |
| 1 |
| (π-x)2 |
| (3π-2x)(4x-3π) |
| (πx-x2)2 |
令f′(x)>0,解得
| 3π |
| 4 |
| 3π |
| 4 |
当且仅当x=
| 3π |
| 4 |
| 3π |
| 4 |
| 12 |
| π |
| 4 |
| π |
| 16 |
| π |
故答案为:
| 16 |
| π |
点评:本题考查了三角形的内角和定理、利用导数研究函数的单调性极值与最值,属于基础题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
(2+x)2+(2+x)3+(2+x)4的展开式中x2的系数是( )
| A、3 | B、10 | C、24 | D、31 |
{an}是等差数列,Sn是其前n项和,a1-a4-a8+2a6+a15=2,则S15=( )
| A、30 | B、15 |
| C、-30 | D、-15 |
函数y=Asin(ωx+ϕ)在一个周期内的图象如右图所示,此函数的解析式为( )
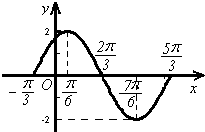

A、y=2sin(x+
| ||||
B、y=2sin(2x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x-
|