题目内容
已知映射f:M→N,使集合N中的元素y=x2与集合M中的元素x对应,要使映射f:M→N是一一对应,那么M,N可以是( )
| A、M=R,N=R |
| B、M=R,N={y|y≥0} |
| C、M={x|x≥0},N=R |
| D、M={x|x≥0},N={y|y≥0} |
考点:映射
专题:函数的性质及应用
分析:根据已知中映射的定义,结合一一对应的概念,逐一进行判断,可得答案.
解答:
解:当M=R,N=R,会出现集合N中的元素y>0与集合M中的元素-x和x对应,集合N中的元素y<0在集合M中不存在对应元素,不满足一一对应,
当M=R,N={y|y≥0},会出现集合N中的元素y>0与集合M中的元素-x和x对应,不满足一一对应,
当M={x|x≥0},N=R,会出现集合N中的元素y<0在集合M中不存在对应元素,不满足一一对应,
当M={x|x≥0},N={y|y≥0},M→N是一一对应,
故选:D
当M=R,N={y|y≥0},会出现集合N中的元素y>0与集合M中的元素-x和x对应,不满足一一对应,
当M={x|x≥0},N=R,会出现集合N中的元素y<0在集合M中不存在对应元素,不满足一一对应,
当M={x|x≥0},N={y|y≥0},M→N是一一对应,
故选:D
点评:本题考查的知识点是映射,难度不大,属于基础题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
{an}是等差数列,Sn是其前n项和,a1-a4-a8+2a6+a15=2,则S15=( )
| A、30 | B、15 |
| C、-30 | D、-15 |
函数y=Asin(ωx+ϕ)在一个周期内的图象如右图所示,此函数的解析式为( )
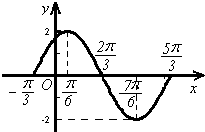

A、y=2sin(x+
| ||||
B、y=2sin(2x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x-
|
双曲线
-
=1(a>0,b>0)与直线y=2x有公共点,则双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||
B、(
| ||
C、(1,
| ||
D、[
|
以下命题不正确的是( )
| A、?x∈N,lgx=2 | ||||
B、双曲线
| ||||
| C、?x∈R,2x-1>0 | ||||
D、抛物线x=2y2的准线方程为x=-
|
圆心为(-2,2),半径为5的圆的标准方程为( )
| A、(x-2)2+(y+2)2=5 |
| B、(x+2)2+(y-2)2=25 |
| C、(x+2)2+(y-2)2=5 |
| D、(x-2)2+(y+2)2=25 |
点(
,0)到直线x-y=0的距离为( )
| 2 |
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|
定义运算:x⊙y=
,如2⊙5=2,则下列等式不能成立的是( )
|
| A、x⊙y=y⊙x |
| B、(x⊙y)⊙z=x⊙(y⊙z) |
| C、(x⊙y)2=x2⊙y2 |
| D、c•(x⊙y)=(c•x)⊙(c•y)(其中c>0) |