题目内容
下列四组函数中,表示同一函数的是( )
A、y=
| |||||
| B、y=1与y=x0 | |||||
| C、y=2x+1与y=2t+1 | |||||
D、y=x与y=(
|
考点:判断两个函数是否为同一函数
专题:函数的性质及应用
分析:根据函数的定义域相同,对应关系也相同,才能判断两个函数是同一函数,对选项中的函数进行判断即可.
解答:
解:对于A,y=
=|x|,y=
=x,它们的对应关系不同,不是同一函数;
对于B,y=1(x∈R),y=x0=1(x≠0),它们的定义域不同,不是同一函数;
对于C,y=2x+1与y=2t+1,它们的定义域相同,对应关系也相同,是同一函数;
对于D,y=x(x∈R),y=(
)2=x(x≥0),它们的定义域不同,不是同一函数.
故选:C.
| x2 |
| 3 | x3 |
对于B,y=1(x∈R),y=x0=1(x≠0),它们的定义域不同,不是同一函数;
对于C,y=2x+1与y=2t+1,它们的定义域相同,对应关系也相同,是同一函数;
对于D,y=x(x∈R),y=(
| x |
故选:C.
点评:不同考查了判断两个函数是否为同一函数的问题,解题时应判断它们的定义域是否相同,对应关系是否也相同,是容易题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
设a=sin
,b=cos
,c=tan
,则( )
| 3π |
| 7 |
| 2π |
| 7 |
| 5π |
| 7 |
| A、b>a>c |
| B、a>b>c |
| C、c>a>b |
| D、b>c>a |
已知函数f(x)=
,则
f(x)dx=( )
|
| ∫ | 2 0 |
| A、4 | ||
| B、3 | ||
| C、2 | ||
D、
|
函数y=Asin(ωx+ϕ)在一个周期内的图象如右图所示,此函数的解析式为( )
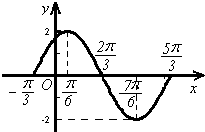

A、y=2sin(x+
| ||||
B、y=2sin(2x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x-
|
设Z=
+(a2+2a-15)i为实数时,实数a的值是( )
| a-5 |
| a2+4a-5 |
| A、3 | B、-5 |
| C、3或-5 | D、-3或5 |
双曲线
-
=1(a>0,b>0)与直线y=2x有公共点,则双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||
B、(
| ||
C、(1,
| ||
D、[
|
圆心为(-2,2),半径为5的圆的标准方程为( )
| A、(x-2)2+(y+2)2=5 |
| B、(x+2)2+(y-2)2=25 |
| C、(x+2)2+(y-2)2=5 |
| D、(x-2)2+(y+2)2=25 |