题目内容
19.求和:${T_n}=1×1+2×2+3×{2^2}+…+n•{2^{n-1}}$=1+(n-1)•2n.分析 利用“错位相减法”、等比数列的求和公式即可得出.
解答 解:${T_n}=1×1+2×2+3×{2^2}+…+n•{2^{n-1}}$,
2Tn=2+2×22+…+(n-1)•2n-1+n•2n,
∴-Tn=1+2+22+…+2n-1-n•2n=$\frac{{2}^{n}-1}{2-1}$-n•2n,
∴${T_n}=1+(n-1){2^n}$,
故答案为:1+(n-1)•2n.
点评 本题考查了“错位相减法”、等比数列的求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.设全集U={1,2,3,4,5,6},集合A={1,3,5},B={4,5,6},则(∁UA)∩B=( )
| A. | {2} | B. | {2,4} | C. | {4,6} | D. | {2,4,6} |
1.已知点A(0,2),抛物线C:y2=ax(a>0)的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,MK垂直准线于点K,若|KM|:|MN|=1:$\sqrt{5}$,则a的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 4 |
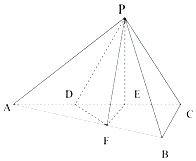 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,点D,E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥平面PBC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,点D,E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥平面PBC.