题目内容
9.设函数f(x)=$\sqrt{{x}^{2}+1}$-ax,其中a>0,证明:当a≥1时,函数f(x)在区间[0,+∞)上是单调函数.分析 当a≥1时,利用函数单调性的定义,即:在区间[0,+∞)上任取x1,x2,使得x1<x2,证明f(x1)-f(x2)>0,从而证明函数f(x)在区间[0,+∞)上是单调减函数.
解答 证明:在区间[0,+∞)上任取x1,x2,
使得x1<x2,f(x1)-f(x2)=$\sqrt{{{x}_{1}}^{2}+1}$-$\sqrt{{{x}_{2}}^{2}+1}$-a(x1-x2)
=(x1-x2)($\frac{{{x}_{1}+x}_{2}}{\sqrt{{{x}_{1}}^{2}+1}+\sqrt{{{x}_{2}}^{2}+1}}$-a),
∵$\frac{{{x}_{1}+x}_{2}}{\sqrt{{{x}_{1}}^{2}+1}+\sqrt{{{x}_{2}}^{2}+1}}$<1,且a≥1,
∴$\frac{{{x}_{1}+x}_{2}}{\sqrt{{{x}_{1}}^{2}+1}+\sqrt{{{x}_{2}}^{2}+1}}$-a<0,
又x1-x2<0,
∴f(x1)-f(x2)>0,
即f(x1)>f(x2),
所以,当a≥1时,函数f(x)在区间[0,+∞)上是单调递减函数.
点评 本小题主要考查不等式的解法、函数的单调性等基本知识,分类讨论的数学思想方法和运算、推理能力.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
1.已知点A(0,2),抛物线C:y2=ax(a>0)的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,MK垂直准线于点K,若|KM|:|MN|=1:$\sqrt{5}$,则a的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 4 |
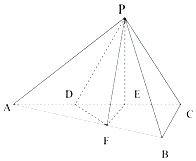 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,点D,E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥平面PBC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,点D,E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥平面PBC.