题目内容
10.点P(1,$\sqrt{2},\sqrt{3}$)为空间直角坐标系中的点,过点P作平面xOy的垂线PQ,垂足为Q,则点Q的坐标为( )| A. | (0,$\sqrt{2}$,0) | B. | (0,$\sqrt{2},\sqrt{3}$) | C. | (1,0,$\sqrt{3}$) | D. | (1,$\sqrt{2}$,0) |
分析 过点(x,y,z)作平面xOy的垂线,垂足的坐标为(x,y,0).
解答 解:∵点P(1,$\sqrt{2},\sqrt{3}$)为空间直角坐标系中的点,
过点P作平面xOy的垂线PQ,垂足为Q,
∴点Q的坐标为(1,$\sqrt{2}$,0).
故选:D.
点评 本题考查空间中点的坐标的求法,是基础题,解题时要认真审题,注意空间直角坐标系的合理运用.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
1.已知点A(0,2),抛物线C:y2=ax(a>0)的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,MK垂直准线于点K,若|KM|:|MN|=1:$\sqrt{5}$,则a的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 4 |
18.已知△ABC的三内角A、B、C所对的边分别是a、b、c,设向量$\overrightarrow{m}$=(a,b),$\overrightarrow{n}$=(sinB,sinA),若$\overrightarrow{m}$$∥\overrightarrow{n}$,且满足(2a-c)cosB=bcosC,则△ABC的形状是( )
| A. | 等腰直角三角形 | B. | 钝角三角形 | C. | 等边三角形 | D. | 直角三角形, |
15.已知集合A={x|log2x>0},B={x|x<2},则( )
| A. | A∩B=∅ | B. | A∪B=R | C. | B⊆A | D. | A⊆B |
20.已知集合A={x|x2-6x+5≤0},B={x|x<a+1}.若A∩B≠∅,则a的取值范围为( )
| A. | (0,+∞) | B. | [0,+∞) | C. | (4,+∞) | D. | [4,+∞) |
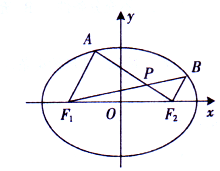 设F1,F2是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),的左右焦点,离心率为$\frac{\sqrt{2}}{2}$,M为椭圆上的动点,|MF1|的最大值为1$+\sqrt{2}$.
设F1,F2是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),的左右焦点,离心率为$\frac{\sqrt{2}}{2}$,M为椭圆上的动点,|MF1|的最大值为1$+\sqrt{2}$.