题目内容
6.在平面直角坐标系xOy中,已知过点M(1,1)的直线l与圆(x+1)2+(y-2)2=5相切,且与直线ax+y-1=0垂直,则实数a=$\frac{1}{2}$.分析 由题意,直线ax+y-1=0的斜率-a=$\frac{2-1}{-1-1}$=-$\frac{1}{2}$,即可得出结论.
解答 解:由题意,直线ax+y-1=0的斜率-a=$\frac{2-1}{-1-1}$=-$\frac{1}{2}$,
∴a=$\frac{1}{2}$.
故答案为$\frac{1}{2}$.
点评 本题考查直线的斜率,考查直线与圆的位置关系,比较基础.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
1.已知点A(0,2),抛物线C:y2=ax(a>0)的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N,MK垂直准线于点K,若|KM|:|MN|=1:$\sqrt{5}$,则a的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 4 |
18.已知△ABC的三内角A、B、C所对的边分别是a、b、c,设向量$\overrightarrow{m}$=(a,b),$\overrightarrow{n}$=(sinB,sinA),若$\overrightarrow{m}$$∥\overrightarrow{n}$,且满足(2a-c)cosB=bcosC,则△ABC的形状是( )
| A. | 等腰直角三角形 | B. | 钝角三角形 | C. | 等边三角形 | D. | 直角三角形, |
15.已知集合A={x|log2x>0},B={x|x<2},则( )
| A. | A∩B=∅ | B. | A∪B=R | C. | B⊆A | D. | A⊆B |
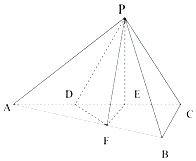 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,点D,E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥平面PBC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,点D,E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥平面PBC.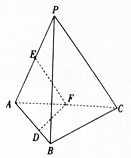 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证:
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,∠BAC=60°,E,F分别是AP,AC的中点,点D在棱AB上,且AD=AC.求证: