题目内容
已知正方形的四个顶点分别为O(0,0),A(1,0),B(1,1),C(0,1),点D,E分别在线段OC,AB上运动,且OD=BE,设AD与OE交于点G,则点G的轨迹方程是( )
| A、y=x(1-x)(0≤x≤1) |
| B、x=y(1-y)(0≤y≤1) |
| C、y=x2(0≤x≤1) |
| D、y=1-x2(0≤x≤1) |
考点:轨迹方程
专题:直线与圆
分析:设出D的坐标,求出直线AD、OE的方程,联立求出交点坐标,消去参数,即可得出点G的轨迹方程.
解答:
解:设D(0,m)(0≤m≤1),则E(1,1-m),
所以直线AD的方程为x+
=1,直线OE的方程为y=(1-m)x,
设G(x,y),
则由
,
可得
,
消去m可得y=(1-x)x(0≤x≤1).
故选A.
所以直线AD的方程为x+
| y |
| m |
设G(x,y),
则由
|
可得
|
消去m可得y=(1-x)x(0≤x≤1).
故选A.
点评:本题考查直线方程,考查两条直线的交点,考查学生的计算能力,确定交点的坐标是关键.

练习册系列答案
相关题目
函数g(x)=lnx-
的零点所在区间是( )
| 1 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
直线
x+y-2=0与圆x2+y2=4相交所得的弦的长为( )
| 3 |
A、2
| ||
B、2
| ||
C、
| ||
D、
|
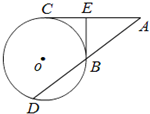 (几何证明选讲选做题)如图,过⊙O外一点A分别作切线AC和割线AD,C为切点,D,B为割线与⊙O的交点,过点B作⊙O的切线交AC于点E.若BE⊥AC,BE=3,AE=4,则DB=
(几何证明选讲选做题)如图,过⊙O外一点A分别作切线AC和割线AD,C为切点,D,B为割线与⊙O的交点,过点B作⊙O的切线交AC于点E.若BE⊥AC,BE=3,AE=4,则DB=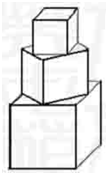 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边中点,已知最底层正方体的棱长为2,且该塔形的表面积(含C最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边中点,已知最底层正方体的棱长为2,且该塔形的表面积(含C最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是