Question

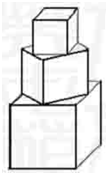有一塔形几何体由若干个正方体构成，构成方式如图所示，上层正方体下底面的四个顶点是下层正方体上底面各边中点，已知最底层正方体的棱长为2，且该塔形的表面积（含C最底层正方体的底面面积）超过39，则该塔形中正方体的个数至少是

 

．

Answer 1

考点：组合几何体的面积、体积问题

专题：计算题

分析：求出各个层的正方体的表面积，求出它们的和，该塔形的表面积（含最底层正方体的底面面积）超过39，求出正方体的个数至少个数．

解答： 解：底层正方体的表面积为24；第2层正方体的棱长2×

2

2

=

2

，每个面的面积为4×

1

2

；第3层正方体的棱长为2×(

2

2

)2，每个面的面积为4×(

1

2

)2；┉，
第n层正方体的棱长为2×(

2

2

)n-1，每个面的面积为4×(

1

2

)n-1；
若该塔形为n层，则它的表面积为24+4×[4×

1

2

+4(

1

2

)2+…+4×(

1

2

)n-1]]=40-(

1

2

)n-5
∵40-(

1

2

)n-5＞39
∴该塔形中正方体的个数至少是6．
故答案是6．

点评：本题是中档题，考查计算能力，数列求和的知识，正确就是解好数学问题的关键．