题目内容

已知椭圆的方程为
y2
9
+
x2
16
=1，则此椭圆的长轴长为（　　）
A、3B、4C、6D、8
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：判断椭圆的焦点坐标所在的轴，然后求解长轴长即可．
解答： 解：椭圆的方程为
y2
9
+
x2
16
=1，焦点坐标在x轴．
所以a=4，2a=8．
此椭圆的长轴长为：8．
故选：D．
点评：本题考查椭圆的基本性质的应用，基本知识的考查．
练习册系列答案
相关题目
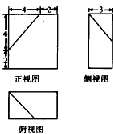
已知某几何体的三视图如上图所示（单位：cm），则该几何体的表面积是（　　）
A、（124+2
34
）cm2
B、92cm2
C、124cm2
D、84cm2
命题：?x，y∈R，如果xy=0，则x=0或y=0的否命题是
 
．
设命题p：关于x的函数y=（a-1）x为增函数，命题q：不等式-3x≤a对一切正实数均成立．
（1）若命题Q为真命题，求实数a的取值范围；
（2）命题“p∨q”为真命题，且“p∧q”为假命题，求实数a的取值范围．
已知数列{an}是等差数列，且a1+a7+a13=2π，则tan（a2+a12）═
 
．
函数f（x）=
4-x2
+
1
lg(x-1)
的定义域是
 
．
已知函数f（x）=-
a
ax+
a
（a＞0，a≠1）的图象关于点（
1
2
，-
1
2
）对称，则f（-3）+f（-2）+f（-1）+f（0）+f（1）+f（2）+f（3）+f（4）=
 
．
已知等差数列{an}的前n项和为Sn，若S3=9，S5=25，则S8=（　　）
A、60B、62C、64D、66
已知
OA
=（4，0），
0B
=（2，2
3
），
OC
=（1-λ）
OA
+λ
OB
（λ2≠λ）
（1）证明A，B，C三点共线，并在
AB
=
BC
时，λ的值；
（2）求|
OC
|的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网