题目内容
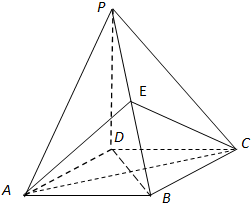 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.(Ⅰ)求证:平面AEC⊥平面PDB;
(Ⅱ)当PD=
| 2 |
考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(Ⅰ)由线面垂直得到PD⊥AC,由正方形性质得到BD⊥AC,所以AC⊥平面PDB,由此能证明平面AEC⊥平面PDB;
(Ⅱ)由已知可得三棱锥A-PDE的高为AO(O为对角线交点在△PDE中面积为△PDB的一半,代入可得答案.
(Ⅱ)由已知可得三棱锥A-PDE的高为AO(O为对角线交点在△PDE中面积为△PDB的一半,代入可得答案.
解答:
(Ⅰ)证明:∵四棱锥底面为正方形,
∴AC⊥BD,
又∵PD⊥底面ABCD,
∴PD⊥AC,
∵BD∩PD=D,
∴AC⊥平面PBD,
∵AC?平面AEC,
∴平面PBD⊥平面AEC;
(Ⅱ)解:由(Ⅰ)知AC⊥平面PBD,∴AC⊥平面PDE,
∴三棱锥A-PDE的高为AO(O为对角线交点),
∵E是PB的中点,
在△PDE中面积为△PDB的一半,
∴S=
×
×2×2=1,
∴VA-PDE=
•S•AO=
.
∴AC⊥BD,
又∵PD⊥底面ABCD,
∴PD⊥AC,
∵BD∩PD=D,
∴AC⊥平面PBD,
∵AC?平面AEC,
∴平面PBD⊥平面AEC;
(Ⅱ)解:由(Ⅰ)知AC⊥平面PBD,∴AC⊥平面PDE,
∴三棱锥A-PDE的高为AO(O为对角线交点),
∵E是PB的中点,
在△PDE中面积为△PDB的一半,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
∴VA-PDE=
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查平面与平面垂直的证明,考查三棱锥A-PED的体积,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
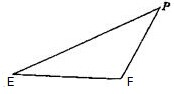 在面积为12的△PEF中,已知tan∠PEF=
在面积为12的△PEF中,已知tan∠PEF=