题目内容
若a＞0，b＞0，且函数f（x）=4x3-ax2-2bx+2在x=1处有极值，求ab的最大值．
考点：函数在某点取得极值的条件
专题：计算题,导数的概念及应用
分析：求出导函数，利用函数在极值点处的导数值为0得到a，b满足的条件，利用基本不等式求出ab的最值．
解答：
解：由题意，求导函数f′（x）=12x2-2ax-2b
∵在x=1处有极值
∴a+b=6
∵a＞0，b＞0
∴ab≤（
）2=9，当且仅当a=b=3时取等号
∴ab的最大值等于9．
∵在x=1处有极值
∴a+b=6
∵a＞0，b＞0
∴ab≤（
| a+b |
| 2 |
∴ab的最大值等于9．
点评：本题考查函数在极值点处的导数值为0、考查利用基本不等式求最值，需注意：一正、二定、三相等．
练习册系列答案
相关题目
函数y=
sin(2x-
)的图象可以看作是函数y=
sin2x的图象（ ）
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
若f（x）是（-a，a）上的可导奇函数，且f'（x）不恒为零，则f'（x）在（-a，a）上（ ）
| A、必为奇函数 |
| B、必为偶函数 |
| C、是非奇非偶函数 |
| D、可能为奇函数，也可能是偶函数 |
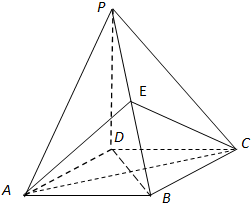如图，四棱锥P-ABCD的底面是正方形，PD⊥底面ABCD，点E在棱PB上．