题目内容
在实数集R上的函数f(x)如果满足:对任意x1,x2∈R,都有f(
)≤
[f(x1)+f(x2)],则称f(x)为R上的凹函数.已知二次函数f(x)=ax2+x(a∈R且a≠0).
(Ⅰ)求证:a>0时,函数f(x)为凹函数;
(Ⅱ)如果x∈(0,1]时,|f(x)|≤1恒成立,试求实数a的取值范围.
| x1+x2 |
| 2 |
| 1 |
| 2 |
(Ⅰ)求证:a>0时,函数f(x)为凹函数;
(Ⅱ)如果x∈(0,1]时,|f(x)|≤1恒成立,试求实数a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(Ⅰ)根据凹函数的定义有f(
)≤
[f(x1)+f(x2)]成立即可;(Ⅱ)问题转化为
在
≥1时恒成立.从而求出a的范围.
| x1+x2 |
| 2 |
| 1 |
| 2 |
|
| 1 |
| x |
解答:
解:(Ⅰ)证明:∵f(x)=ax2+x(a∈R且a≠0),
∴对任意x1,x2∈R,有
∴f(
)≤
[f(x1)+f(x2)]
故函数f(x)=ax2+x(a>0)为R上的凹函数
(Ⅱ)∵x∈(0,1]时,|f(x)|≤1恒成立,∴x∈(0,1]时,-1≤ax2+x≤1恒成立.
∵0<x≤1,∴
≥1,问题转化为
在
≥1时恒成立.
∵
-
=(
-
)2-
在
=1时取得最小值0,∴a≤0,
又∵
+
=(
+
)2-
在
=1时取得最小值2,
∴-a≤2,即a≥-2,
又a≠0,故a∈[-2,0).
∴对任意x1,x2∈R,有
|
∴f(
| x1+x2 |
| 2 |
| 1 |
| 2 |
故函数f(x)=ax2+x(a>0)为R上的凹函数
(Ⅱ)∵x∈(0,1]时,|f(x)|≤1恒成立,∴x∈(0,1]时,-1≤ax2+x≤1恒成立.
∵0<x≤1,∴
| 1 |
| x |
|
| 1 |
| x |
∵
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| x |
又∵
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| x |
∴-a≤2,即a≥-2,
又a≠0,故a∈[-2,0).
点评:本题考查了二次函数的性质,考查新定义问题,考查不等式的问题,本题属于中档题.

练习册系列答案
相关题目
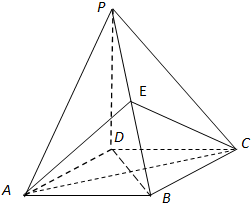 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.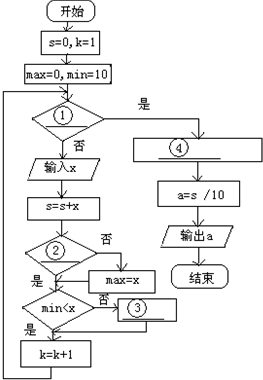 “钦州一中好声音”共有4名教师选手进入决赛,请了12名评委,在计算每位选手的平均分数时,去掉一个最高分和一个最低分后再求平均分.以下是一个程序框图,设计了一个算法,用循环语句完成这12个分数的输入,累加变量求和后减去最大数与最小数再求平均值.(假定分数采用10分制,即每位选手的分数最高分为10分,最低分为0分).
“钦州一中好声音”共有4名教师选手进入决赛,请了12名评委,在计算每位选手的平均分数时,去掉一个最高分和一个最低分后再求平均分.以下是一个程序框图,设计了一个算法,用循环语句完成这12个分数的输入,累加变量求和后减去最大数与最小数再求平均值.(假定分数采用10分制,即每位选手的分数最高分为10分,最低分为0分).