题目内容
某地区有小学21所,中学14所,大学7所,现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(Ⅰ)求应从小学、中学、大学中分别抽取的学校数目.
(Ⅱ)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率.
(Ⅰ)求应从小学、中学、大学中分别抽取的学校数目.
(Ⅱ)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)利用分层抽样的意义,先确定抽样比,在确定每层中抽取的学校数目;
(Ⅱ)(1)从抽取的6所学校中随机抽取2所学校,所有结果共有
=15种,按规律列举即可;
(2)先列举抽取结果两所学校均为小学的基本事件数,再利用古典概型概率的计算公式即可得结果
(Ⅱ)(1)从抽取的6所学校中随机抽取2所学校,所有结果共有
| C | 2 6 |
(2)先列举抽取结果两所学校均为小学的基本事件数,再利用古典概型概率的计算公式即可得结果
解答:
解:(I)抽样比为
=
,
故应从小学、中学、大学中分别抽取的学校数目分别为21×
=3,14×
=2,7×
=1
(II)(1)在抽取到的6所学校中,3所小学分别记为1、2、3,两所中学分别记为a、b,大学记为A
则抽取2所学校的所有可能结果为{1,2},{1,3},{1,a},{1,b},{1,A},{2,3},{2,a},{2,b},{2,A},{3,a},{3,b},{3,A},{a,b},{a,A},{b,A},共15种
(2)设B={抽取的2所学校均为小学},事件B的所有可能结果为{1,2},{1,3},{2,3}共3种,
∴P(B)=
=
| 6 |
| 21+14+7 |
| 1 |
| 7 |
故应从小学、中学、大学中分别抽取的学校数目分别为21×
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 7 |
(II)(1)在抽取到的6所学校中,3所小学分别记为1、2、3,两所中学分别记为a、b,大学记为A
则抽取2所学校的所有可能结果为{1,2},{1,3},{1,a},{1,b},{1,A},{2,3},{2,a},{2,b},{2,A},{3,a},{3,b},{3,A},{a,b},{a,A},{b,A},共15种
(2)设B={抽取的2所学校均为小学},事件B的所有可能结果为{1,2},{1,3},{2,3}共3种,
∴P(B)=
| 3 |
| 15 |
| 1 |
| 5 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
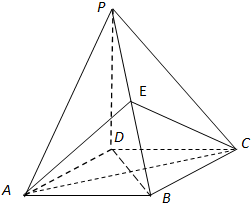 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.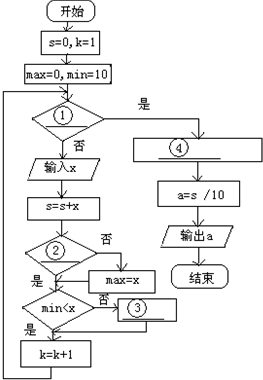 “钦州一中好声音”共有4名教师选手进入决赛,请了12名评委,在计算每位选手的平均分数时,去掉一个最高分和一个最低分后再求平均分.以下是一个程序框图,设计了一个算法,用循环语句完成这12个分数的输入,累加变量求和后减去最大数与最小数再求平均值.(假定分数采用10分制,即每位选手的分数最高分为10分,最低分为0分).
“钦州一中好声音”共有4名教师选手进入决赛,请了12名评委,在计算每位选手的平均分数时,去掉一个最高分和一个最低分后再求平均分.以下是一个程序框图,设计了一个算法,用循环语句完成这12个分数的输入,累加变量求和后减去最大数与最小数再求平均值.(假定分数采用10分制,即每位选手的分数最高分为10分,最低分为0分).