题目内容
已知f(x)是定义在(0,+∞)上的增函数,且对任意的x>0,y>0都满足f(
)=f(x)-f(y).
(1)求f(1)的值;
(2)若x>0,证明f(x2)=2f(x);
(3)若f(3)=1,解不等式f(x+3)-f(
)<2.
| x |
| y |
(1)求f(1)的值;
(2)若x>0,证明f(x2)=2f(x);
(3)若f(3)=1,解不等式f(x+3)-f(
| 1 |
| x-1 |
考点:抽象函数及其应用,函数单调性的性质
专题:函数的性质及应用,不等式的解法及应用
分析:(1)利用赋值法,令x=y=1,即可求出f(1)=0,
(2)先令y=
,代入化简即可证明,
(3)先求出f(9)=2,再化简不等式,根据函数在(0,+∞)上的增函数,构造不等式组,解得即可
(2)先令y=
| 1 |
| x |
(3)先求出f(9)=2,再化简不等式,根据函数在(0,+∞)上的增函数,构造不等式组,解得即可
解答:
解:(1)令x=y=1,得f(1)=f(1)-f(1)=0;
(2)令y=
,
∴f(
)=f(
)=f(x2)=f(x)-f(
)=f(x)-f(1)+f(x)=2f(x)
(3)由(2)得,f(32)=f(9)=2f(3)=2
∵f(x+3)-f(
)<2.
∴f[(x+3)(x-1)]=f(x2+2x-3)<f(9)
∵f(x)是定义在(0,+∞)上的增函数,
∴
解得1<x<-1+
所以不等式的解集为(1,-1+
)
(2)令y=
| 1 |
| x |
∴f(
| x |
| y |
| x | ||
|
| 1 |
| x |
(3)由(2)得,f(32)=f(9)=2f(3)=2
∵f(x+3)-f(
| 1 |
| x-1 |
∴f[(x+3)(x-1)]=f(x2+2x-3)<f(9)
∵f(x)是定义在(0,+∞)上的增函数,
∴
|
解得1<x<-1+
| 13 |
所以不等式的解集为(1,-1+
| 13 |
点评:本题考查抽象函数及其应用,考查赋值法,突出考查函数单调性的应用与解不等式组的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
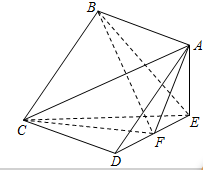 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点. 已知函数g(x)=ex(e=2.718…)的图象如图所示.
已知函数g(x)=ex(e=2.718…)的图象如图所示.