题目内容
已知sinα=-
，且π＜α＜
，求角α的其它两个三角函数值．
| 5 |
| 13 |
| 3π |
| 2 |
考点：同角三角函数间的基本关系
专题：三角函数的求值
分析：由条件利用同角三角函数的基本关系，以及三角函数在各个象限中的符号，求得角α的其他两个三角函数值．
解答：
解：∵已知sinα=-
，且π＜α＜
，则cosα=-
=-
，tanα=
=
．
| 5 |
| 13 |
| 3π |
| 2 |
| 1-sin2α |
| 12 |
| 13 |
| sinα |
| cosα |
| 5 |
| 12 |
点评：本题主要考查同角三角函数的基本关系，以及三角函数在各个象限中的符号，属于基础题．
练习册系列答案
相关题目
△ABC中，cosA=
，则△ABC形状是（ ）
| b |
| c |
| A、正三角形 |
| B、直角三角形 |
| C、等腰三角形或直角三角形 |
| D、等腰直角三角形 |
已知直线l1的方向向量
=（2，4，x），直线l2的方向向量
=（2，y，2），若|
|=6，且
⊥
，则x+y的值是（ ）
| a |
| b |
| a |
| a |
| b |
| A、-3或1 | B、3或-1 |
| C、-3 | D、1 |
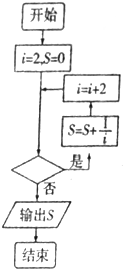如图，给出的是计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 2016 |
| A、i≤2021 |
| B、i≤2019 |
| C、i≤2017 |
| D、i≤2015 |
函数y=|sinx|的一个单调递增区间是（ ）
A、（
| ||
| B、（π，2π） | ||
C、（π，
| ||
| D、（0，π） |