题目内容
函数y=x+
的值域为 .
| 1+x2 |
考点:函数的值域
专题:函数的性质及应用
分析:利用放缩法,即可求出函数的值域
解答:
解:∵y=y=x+
>x+
=x+|x|≥0
∴值域为(0,+∞)
故答案为:(0,+∞)
| 1+x2 |
| x2 |
∴值域为(0,+∞)
故答案为:(0,+∞)
点评:本题考查了函数的值域的求法,属于基础题

练习册系列答案
相关题目
已知向量
=(0,sinx),
=(1,2cosx),函数f(x)=
•
,g(x)=
2+
2-
,则f(x)的图象可由g(x)的图象经过怎样的变换得到( )
| a |
| b |
| 3 |
| 2 |
| a |
| b |
| a |
| b |
| 7 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
已知定义在R上的奇函数f(x)是以π为最小正周期的周期函数,且当x∈[0,
]时,f(x)=sinx,则f(
)的值为( )
| π |
| 2 |
| 5π |
| 3 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
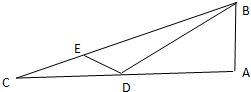 如图,在Rt△ABC中,∠A=90°,D是AC上一点,E是BC上一点,若AB=
如图,在Rt△ABC中,∠A=90°,D是AC上一点,E是BC上一点,若AB=