题目内容
 已知函数g(x)=ex(e=2.718…)的图象如图所示.
已知函数g(x)=ex(e=2.718…)的图象如图所示.(Ⅰ)在所给坐标系中画出φ(x)=(e-1)x+1的图象;
(Ⅱ)利用(Ⅰ)中所做的图象,比较g(0.9)与φ(0.9)的大小;
(Ⅲ)若f(x)=lnx+2x-6只在区间(2,3)内有意义且连续,判断f(x)=lnx+2x-6在区间(2,3)内存在零点c,并找出零点c的近似值x0所在的一个区间,使得|x0-c|<0.1.
考点:指数函数的图像与性质,二分法求方程的近似解
专题:函数的性质及应用
分析:(Ⅰ)由φ(x)的解析式化简φ(x)的图象;
(Ⅱ)作直线x=0.9分别交g(x)和φ(x)与A、B两点,由图象即可判断出g(0.9)与φ(0.9)的大小;
(Ⅲ)先求出f(2.5)和f(e)的值并判断出符号,由函数零点存在性判定定理得:f(x)在区间(2.5,e)内存在零点c,即f(x)在区间(2,3)内存在零点c,由g(0.9)<φ(0.9)得e0.9<2.6,再得f(2.6)>0,
将零点所在的区间进一步缩小为(2.5,2.6),即可得到结论.
(Ⅱ)作直线x=0.9分别交g(x)和φ(x)与A、B两点,由图象即可判断出g(0.9)与φ(0.9)的大小;
(Ⅲ)先求出f(2.5)和f(e)的值并判断出符号,由函数零点存在性判定定理得:f(x)在区间(2.5,e)内存在零点c,即f(x)在区间(2,3)内存在零点c,由g(0.9)<φ(0.9)得e0.9<2.6,再得f(2.6)>0,
将零点所在的区间进一步缩小为(2.5,2.6),即可得到结论.
解答:
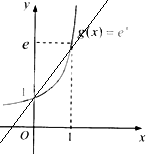 解:(Ⅰ)如图,
解:(Ⅰ)如图,
φ(x)=(e-1)x+1的图象是一条过(0,1)和(1,e)的直线;
(Ⅱ)如图: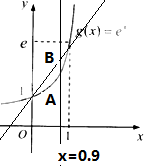 作直线x=0.9分别交g(x)和φ(x)与A、B两点,
作直线x=0.9分别交g(x)和φ(x)与A、B两点,
因为B在A点的上方,所以g(0.9)<φ(0.9);
(Ⅲ)因为f(x)在区间(2,3)上连续,所以在区间[2.5,e]上也连续,
∵f(2.5)=ln2.5+5-6=ln2.5-1<lne-1=0,
f(e)=lne+2e-6>1+2×2.7-6=0.4>0,
∴f(2.5)f(e)<0,
所以f(x)在区间(2.5,e)内存在零点c,
即f(x)在区间(2,3)内存在零点c,
∵φ(0.9)=(e-1)×0.9+1=0.9e+0.1<0.9×2.72+0.1=2.548<2.6,
又g(0.9)<φ(0.9),则e0.9<2.6,所以0.9<ln2.6,
∵f(2.6)=ln2.6+2-6=ln2.6-0.8>0.9-0.8=0.1>0,
∴f(2.5)f(2.6)<0,所以零点c∈(2.5,2.6),
若取零点c的近似值x0所在的一个区间为(2.5,2.6),
则|x0-c|<|2.6-2.5|=0.1,
所以零点c的近似值x0可取区间为(2.5,2.6).
 解:(Ⅰ)如图,
解:(Ⅰ)如图,φ(x)=(e-1)x+1的图象是一条过(0,1)和(1,e)的直线;
(Ⅱ)如图:
 作直线x=0.9分别交g(x)和φ(x)与A、B两点,
作直线x=0.9分别交g(x)和φ(x)与A、B两点,因为B在A点的上方,所以g(0.9)<φ(0.9);
(Ⅲ)因为f(x)在区间(2,3)上连续,所以在区间[2.5,e]上也连续,
∵f(2.5)=ln2.5+5-6=ln2.5-1<lne-1=0,
f(e)=lne+2e-6>1+2×2.7-6=0.4>0,
∴f(2.5)f(e)<0,
所以f(x)在区间(2.5,e)内存在零点c,
即f(x)在区间(2,3)内存在零点c,
∵φ(0.9)=(e-1)×0.9+1=0.9e+0.1<0.9×2.72+0.1=2.548<2.6,
又g(0.9)<φ(0.9),则e0.9<2.6,所以0.9<ln2.6,
∵f(2.6)=ln2.6+2-6=ln2.6-0.8>0.9-0.8=0.1>0,
∴f(2.5)f(2.6)<0,所以零点c∈(2.5,2.6),
若取零点c的近似值x0所在的一个区间为(2.5,2.6),
则|x0-c|<|2.6-2.5|=0.1,
所以零点c的近似值x0可取区间为(2.5,2.6).
点评:本题考查一次函数的图象,函数零点存在性判定定理,数形结合思想思想,考查计算化简能力,属于中档题.

练习册系列答案
相关题目
函数y=|sinx|的一个单调递增区间是( )
A、(
| ||
| B、(π,2π) | ||
C、(π,
| ||
| D、(0,π) |
已知定义在R上的奇函数f(x)是以π为最小正周期的周期函数,且当x∈[0,
]时,f(x)=sinx,则f(
)的值为( )
| π |
| 2 |
| 5π |
| 3 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
斜率为3,在y轴上的截距为4的直线方程是( )
| A、3x-y+4=0 |
| B、x-3y-12=0 |
| C、3x-y-4=0 |
| D、3x-y-12=0 |
 如图所示为函数f(x)=Asin(ωx+φ)( A>0,ω>0,0≤φ≤π)的部分图象,那么f(-3)=( )
如图所示为函数f(x)=Asin(ωx+φ)( A>0,ω>0,0≤φ≤π)的部分图象,那么f(-3)=( )A、-
| ||
| B、0 | ||
| C、-1 | ||
| D、1 |