题目内容
已知△ABC中,角A,B,C的对边分别为a,b,c,若acosC,bcosB,ccosA依次成等差数列.
(1)求角B;
(2)若△ABC的外接圆面积为π,求△ABC面积的最大值.
(1)求角B;
(2)若△ABC的外接圆面积为π,求△ABC面积的最大值.
考点:余弦定理,正弦定理
专题:计算题,等差数列与等比数列,解三角形,不等式的解法及应用
分析:(1)利用等差数列的性质以及正弦定理,结合两角和的正弦公式和内角和定理,求出B的余弦值,然后求角B的大小;
(2)由△ABC的外接圆的面积为π,求出半径,利用正弦定理可得b,再利用余弦定理,结合基本不等式,即可求△ABC面积的最大值.
(2)由△ABC的外接圆的面积为π,求出半径,利用正弦定理可得b,再利用余弦定理,结合基本不等式,即可求△ABC面积的最大值.
解答:
解:(1)∵acosC,bcosB,ccosA依次成等差数列.
∴acosC+ccosA=2bcosB,
∴sinAcosC+sinCcosA=2sinBcosB,
∴sin(A+C)=2sinBcosB,
则sinB=2sinBcosB,
∴cosB=
,
由于0<B<π,则B=
;
(2)∵△ABC的外接圆的面积为π,
∴r=1,
∴b=2rsinB=2×1×
=
,
∴3=a2+c2-2accosB≥ac,
当且仅当a=c时,取等号,即ac的最大值为3,
∴△ABC面积为
acsinB≤
×3×
=
.
则△ABC面积的最大值为
.
∴acosC+ccosA=2bcosB,
∴sinAcosC+sinCcosA=2sinBcosB,
∴sin(A+C)=2sinBcosB,
则sinB=2sinBcosB,
∴cosB=
| 1 |
| 2 |
由于0<B<π,则B=
| π |
| 3 |
(2)∵△ABC的外接圆的面积为π,
∴r=1,
∴b=2rsinB=2×1×
| ||
| 2 |
| 3 |
∴3=a2+c2-2accosB≥ac,
当且仅当a=c时,取等号,即ac的最大值为3,
∴△ABC面积为
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
则△ABC面积的最大值为
3
| ||
| 4 |
点评:本题考查正弦定理、余弦定理的运用,考查三角形的内角和定理的应用,考查基本不等式的运用:求最值,注意角的范围的应用,考查计算能力.

练习册系列答案
相关题目
已知全集U={0,1,2,3},A={1,3},则集合∁UA=( )
| A、{0} |
| B、{1,2} |
| C、{0,2} |
| D、{0,1,2} |
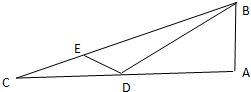 如图,在Rt△ABC中,∠A=90°,D是AC上一点,E是BC上一点,若AB=
如图,在Rt△ABC中,∠A=90°,D是AC上一点,E是BC上一点,若AB=