题目内容
已知圆C与直线l:x+y=1相切于点A(2,1)且圆心在直线y=-2x上,
(1)求圆C的方程;
(2)过点B(3,2)作圆C的切线,求该切线方程.
(1)求圆C的方程;
(2)过点B(3,2)作圆C的切线,求该切线方程.
考点:圆的标准方程,圆的切线方程
专题:直线与圆
分析:(1)设圆心C的坐标为(a,-2a),根据直线AC和直线l垂直求得a的值,可得圆心C的坐标,根据半径为圆心C到切线l的距离,求得半径r的值,可得圆C的方程.
(2)由条件利用点斜式求得此切线的方程,再根据圆心C(
,-
)到此切线的距离等于半径求得斜率k的值,可得该切线方程.
(2)由条件利用点斜式求得此切线的方程,再根据圆心C(
| 1 |
| 3 |
| 2 |
| 3 |
解答:
解:(1)设圆心C的坐标为(a,-2a),根据直线AC和直线l垂直可得
•(-1)=-1,
求得a=
,可得C(
,-
),且半径为圆心C到切线l的距离,即半径r=
=
,
故圆C的方程为 (x-
)2+(y+
)2=
.
(2)设过点B(3,2)的切线的斜率为k,则此切线的方程为y-2=k(x-3),即 kx-y+2-3k=0.
再根据圆心C(
,-
)到此切线的距离等于半径,可得
=
,
求得k=
,或k=
,
故该切线方程为
x-y+2-
=0,或
x-y+2-
=0.
| -2a-1 |
| a-2 |
求得a=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
|
| ||||
|
2
| ||
| 3 |
故圆C的方程为 (x-
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 9 |
(2)设过点B(3,2)的切线的斜率为k,则此切线的方程为y-2=k(x-3),即 kx-y+2-3k=0.
再根据圆心C(
| 1 |
| 3 |
| 2 |
| 3 |
|
| ||||
|
2
| ||
| 3 |
求得k=
8+
| ||
| 7 |
8-
| ||
| 7 |
故该切线方程为
8+
| ||
| 7 |
24+3
| ||
| 5 |
8+
| ||
| 7 |
24-3
| ||
| 7 |
点评:本题主要考查求圆的标准方程的方法,求出圆心坐标和半径的值,是解题的关键.还考查了直线和圆相切的性质,点到直线的距离公式的应用,属于中档题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
已知直线l1的方向向量
=(2,4,x),直线l2的方向向量
=(2,y,2),若|
|=6,且
⊥
,则x+y的值是( )
| a |
| b |
| a |
| a |
| b |
| A、-3或1 | B、3或-1 |
| C、-3 | D、1 |
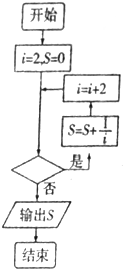 如图,给出的是计算
如图,给出的是计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 2016 |
| A、i≤2021 |
| B、i≤2019 |
| C、i≤2017 |
| D、i≤2015 |
斜率为3,在y轴上的截距为4的直线方程是( )
| A、3x-y+4=0 |
| B、x-3y-12=0 |
| C、3x-y-4=0 |
| D、3x-y-12=0 |