题目内容
已知一次函数f(x),满足f(1)=0,f(3)=-2,
(1)求函数解析式,作出函数f(x)的图象;
(2)求函数f(x)在x∈[-1,2)的值域.
(1)求函数解析式,作出函数f(x)的图象;
(2)求函数f(x)在x∈[-1,2)的值域.
考点:函数解析式的求解及常用方法,函数的值域
专题:函数的性质及应用
分析:(1)设出函数的表达式,得方程组,解出a,b的值即可;(2)根据函数的单调性求出函数的值域.
解答:
解:(1)设f(x)=ax+b,
由f(1)=0,f(3)=-2,
得:
,解得:
,
∴f(x)=-x+1,
如图示:
 ;
;
(2)由(1)得:f(x)在[-1,2)递减,
∴f(x)max=f(-1)=2,f(x)min=f(2)=-1,
∴函数f(x)在x∈[-1,2)的值域是(-1,2].
由f(1)=0,f(3)=-2,
得:
|
|
∴f(x)=-x+1,
如图示:
 ;
;(2)由(1)得:f(x)在[-1,2)递减,
∴f(x)max=f(-1)=2,f(x)min=f(2)=-1,
∴函数f(x)在x∈[-1,2)的值域是(-1,2].
点评:本题考查了求函数的解析式问题,考查了函数的图象,值域问题,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=
+
的两个极值点分别为x1,x2,且x1∈(0,1),x2∈(1,+∞),点P(m,n)表示的平面区域为D,若函数y=loga(x+4)(a>1)的图象上存在区域D内的点,则实数a的取值范围为( )
| x3 |
| 3 |
| mx2+(m+n)x+1 |
| 2 |
| A、(1,3] |
| B、(1,3) |
| C、(3,+∞) |
| D、[3,+∞) |
当a>0时,函数f(x)=(x2-ax)ex的图象大致是( )
A、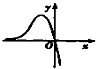 |
B、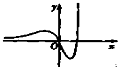 |
C、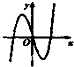 |
D、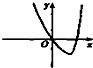 |
函数f(x)=4lnx-x2的大致图象是( )
A、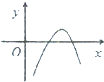 |
B、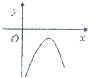 |
C、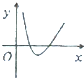 |
D、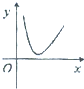 |
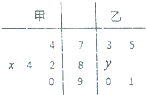 某中学高二年级的甲、乙两个班中,需根据某次数学预赛成绩选出某班的5名学生参加数学竞赛决赛,已知这次预赛他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班5名学生成绩的平均分是83,乙班5名学生成绩的中位数是86.
某中学高二年级的甲、乙两个班中,需根据某次数学预赛成绩选出某班的5名学生参加数学竞赛决赛,已知这次预赛他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班5名学生成绩的平均分是83,乙班5名学生成绩的中位数是86.