题目内容
已知函数f（x）=-x2+2mx+1，若?x0∈R，使得?x1∈[1，2]都有f（x1）＜f（x0），则实数m的取值范围是 ．
考点：二次函数的性质
专题：函数的性质及应用
分析：函数f（x）=-x2+2mx+1开口向下、对称轴方程为x=m的抛物线，由?x0∈R，使得?x1∈[1，2]都有f（x1）＜f（x0），知m＜1或m＞2．
解答：
解：函数f（x）=-x2+2mx+1开口向下、对称轴方程为x=m的抛物线，
∵?x0∈R，使得?x1∈[1，2]都有f（x1）＜f（x0），
结合抛物线的形状：
如图示：
∴m＜1或m＞2，
故答案为：（-∞，1）∪（2，+∞）．
∵?x0∈R，使得?x1∈[1，2]都有f（x1）＜f（x0），
结合抛物线的形状：
如图示：
∴m＜1或m＞2，
故答案为：（-∞，1）∪（2，+∞）．
点评：本题考查二次函数的性质，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
轻松暑假总复习系列答案
相关题目
已知一元二次函数f（x）=x2+bx+c，且不等式x2+bx+c＞0的解集为{x|x＜-1或x＞
}，则f（10x）＞0的解集为（ ）
| 1 |
| 2 |
| A、{x|x＜-1或x＞lg2} |
| B、{x|-1＜x＜lg2} |
| C、{x|x＞-lg2} |
| D、{x|x＜-lg2} |
如图，点E，F分别是锐角∠A两边上的点，AE=AF，分别以点E，F为圆心，以AE的长为半径画弧，两弧相交于点D，连接DE，DF．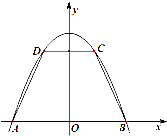
如图，抛物线y=-x2+9与x轴交于两点A，B，点C，D在抛物线上（点C在第一象限），CD∥AB．记|CD|=2x，梯形ABCD面积为S．在△ABC中，内角A，B，C所对的边分别是a，b，c，已知b-c=
a，2sinB=3sinC，则cosA=（ ）
| 1 |
| 4 |
A、-
| ||
B、
| ||
C、
| ||
D、
|