题目内容
若函数y=f（x）在R单调递减，且f（2a+2）＞f（a2-1），则实数a的取值范围是 ．
考点：函数单调性的性质
专题：函数的性质及应用
分析：根据函数f（x）的单调性可去掉不等式f（2a+2）＞f（a2-1）中的符号“f”，从而可解出a的范围．
解答：
解：因为函数f（x）是R上的单调递减函数，
所以f（2a+2）＞f（a2-1）可化为：
2a+2＜a2-1，即a2-2a-3＞0，
所以实数a的取值范围是{a|a＞3或a＜-1}．
故答案为：{a|a＞3或a＜-1}
所以f（2a+2）＞f（a2-1）可化为：
2a+2＜a2-1，即a2-2a-3＞0，
所以实数a的取值范围是{a|a＞3或a＜-1}．
故答案为：{a|a＞3或a＜-1}
点评：本题考查函数的单调性，及应用单调性解抽象不等式问题，属基础题．
练习册系列答案
相关题目
已知一元二次函数f（x）=x2+bx+c，且不等式x2+bx+c＞0的解集为{x|x＜-1或x＞
}，则f（10x）＞0的解集为（ ）
| 1 |
| 2 |
| A、{x|x＜-1或x＞lg2} |
| B、{x|-1＜x＜lg2} |
| C、{x|x＞-lg2} |
| D、{x|x＜-lg2} |
在△ABC中，内角A，B，C所对的边分别是a，b，c，已知b-c=
a，2sinB=3sinC，则cosA=（ ）
| 1 |
| 4 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
函数y=2x-x2的图象大致是（ ）
A、 |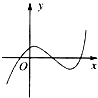
B、 |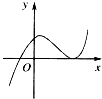
C、 |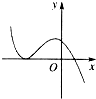
D、 |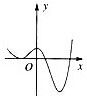
（文）若a∈R，则“a2＞a”是“a＞1”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
函数f（x）=
，则
f（x）dx的值为（ ）
|
| ∫ | 2 -2 |
| A、π+6 | B、π-2 | C、2π | D、8 |
若定义在R上的函数f（x）满足：对任意x1，x2∈R有f（x1+x2）=f（x1）+f（x2）+1，则下列说法一定正确的是（ ）
| A、f（x）-1是奇函数 |
| B、f（x）-1是偶函数 |
| C、f（x）+1是奇函数 |
| D、f（x）+1是偶函数 |