题目内容
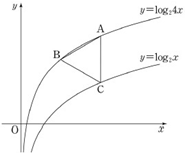 如图所示,已知函数y=log24x图象上的两点A,B和函数y=log2x上的点 C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为(p,q),则实数p的值为
如图所示,已知函数y=log24x图象上的两点A,B和函数y=log2x上的点 C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为(p,q),则实数p的值为考点:对数函数的图像与性质
专题:函数的性质及应用
分析:根据题意,设出A、B、C的坐标,由线段AC∥y轴,△ABC是等边三角形,得出AB、AC与BC的关系,求出p、q的值,计算出结果.
解答:
解:根据题意,设A(x0,2+log2x0),B(p,q),C(x0,log2x0),
∵线段AC∥y轴,△ABC是等边三角形,
∴AC=2,2+log2p=q,
∴p=2q-2,∴4p=2q;
又x0-p=
,∴p=x0-
,
∴x0=p+
;
又2+log2x0-q=1,
∴log2x0=q-1,x0=2q-1;
∴p+
=2q-1;2p+2=2q=4p,
∴p=
,
故答案为:
.
∵线段AC∥y轴,△ABC是等边三角形,
∴AC=2,2+log2p=q,
∴p=2q-2,∴4p=2q;
又x0-p=
| 3 |
| 3 |
∴x0=p+
| 3 |
又2+log2x0-q=1,
∴log2x0=q-1,x0=2q-1;
∴p+
| 3 |
∴p=
| 3 |
故答案为:
| 3 |
点评:本题考查了指数函数与对数函数的图象与性质的应用问题,也考查了指数,对数的运算问题,属于中档题.

练习册系列答案
相关题目
已知点(1,1)、(0,-2)在直线x+ay+1=0的两侧,则实数a的取值范围( )
A、(-2,-
| ||
B、(-∞,-2)∪(-
| ||
C、(-2,
| ||
D、(-∞,-2)∪(
|
椭圆x2+
=1的一个焦点是(0,
),那么k=( )
| y2 |
| k |
| 5 |
| A、-6 | ||
| B、6 | ||
C、
| ||
D、1-
|
函数f(x)是定义在R上的奇函数,当x>0时,f(x)=x2+1,则f(-1)等于( )
| A、1 | B、-1 | C、2 | D、-2 |
设数列{an}是等比数列,函数y=x2-x-2的两个零点是a2,a3,则a1a4=( )
| A、2 | B、1 | C、-1 | D、-2 |
下列各组函数中表示相同函数的是( )
A、y=
| |||||
| B、y=lnex与y=elnx | |||||
C、y=
| |||||
D、y=x0与y=
|