题目内容
设数列{an}是等比数列，函数y=x2-x-2的两个零点是a2，a3，则a1a4=（ ）
| A、2 | B、1 | C、-1 | D、-2 |
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：由韦达定理和等比数列的性质可得a1a4=a2a3=-2
解答：
解：∵函数y=x2-x-2的两个零点是a2，a3，
∴a2a3=-2
又∵数列{an}是等比数列，
∴a1a4=a2a3=-2
故选：D
∴a2a3=-2
又∵数列{an}是等比数列，
∴a1a4=a2a3=-2
故选：D
点评：本题考查等比数列的性质和韦达定理，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
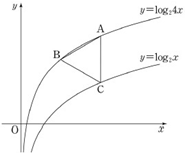如图所示，已知函数y=log24x图象上的两点A，B和函数y=log2x上的点 C，线段AC平行于y轴，三角形ABC为正三角形时，点B的坐标为（p，q），则实数p的值为在0°～360°之间，与角-150°终边相同的角是（ ）
| A、150° | B、-30° |
| C、30° | D、210° |
函数y=1-2x（x≤0）的值域是（ ）
| A、（0，1） |
| B、（-∞，1） |
| C、（0，1] |
| D、[0，1） |