题目内容
下列各组函数中表示相同函数的是( )
A、y=
| |||||
| B、y=lnex与y=elnx | |||||
C、y=
| |||||
D、y=x0与y=
|
考点:判断两个函数是否为同一函数
专题:计算题,函数的性质及应用
分析:由定义域及对应关系判断函数相同.
解答:
解:y=
=x与y=
=|x|;对应关系不同,
y=lnex的定义域为R,y=elnx的定义域为(0,+∞),故不同;
y=
的定义域为{x|x≠1},y=x+3的定义域为R,故不同;
y=x0=1与y=
=1,定义域都是{x|x≠0},故相同;
故选D.
| 3 | x3 |
| x2 |
y=lnex的定义域为R,y=elnx的定义域为(0,+∞),故不同;
y=
| (x-1)(x+3) |
| x-1 |
y=x0=1与y=
| 1 |
| x0 |
故选D.
点评:本题考查了函数相同的判断,属于基础题.

练习册系列答案
相关题目
函数y=1-2x(x≤0)的值域是( )
| A、(0,1) |
| B、(-∞,1) |
| C、(0,1] |
| D、[0,1) |
已知向量
=(sin67°cos37°,cos37°cos67°),
=(-cos67°sin37°,sin37°sin67°),
=(1,t),若
∥(
+
),则t=( )
| a |
| b |
| c |
| c |
| a |
| b |
A、
| ||||
B、2
| ||||
C、3
| ||||
D、
|
已知复数z满足z(2+i)=2-i,则z=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
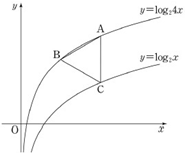 如图所示,已知函数y=log24x图象上的两点A,B和函数y=log2x上的点 C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为(p,q),则实数p的值为
如图所示,已知函数y=log24x图象上的两点A,B和函数y=log2x上的点 C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为(p,q),则实数p的值为