题目内容
已知圆M的圆心M在x轴上,半径为2,直线l:3x-4y+1=0被圆M截得的弦长为2
,且圆心M在直线l的上方.
(1)求圆M的方程;
(2)设A(0,t),B(0,t+6)(-4≤t≤-2),若圆M是△ABC的内切圆,求△ABC的面积S的最大值及对应的t值.
| 3 |
(1)求圆M的方程;
(2)设A(0,t),B(0,t+6)(-4≤t≤-2),若圆M是△ABC的内切圆,求△ABC的面积S的最大值及对应的t值.
考点:圆的标准方程,三角形的面积公式
专题:综合题,直线与圆
分析:(1)设圆心M(a,0),利用M到l:3x-4y+1=0的距离,求出M坐标,然后求圆M的方程;
(2)设AC斜率为k1,BC斜率为k2,推出直线AC、直线BC的方程,求出△ABC的面积S的表达式,求出面积的最大值.
(2)设AC斜率为k1,BC斜率为k2,推出直线AC、直线BC的方程,求出△ABC的面积S的表达式,求出面积的最大值.
解答:
解:(1)设圆心M(a,0),由已知,得M到l:3x-4y+1=0的距离为
=1,∴
=1,
又∵M在l的上方,∴3a+1<0,∴-3a-1=5,∴a=-2,故圆的方程为(x+2)2+y2=4;
(2)设AC斜率为k1,BC斜率为k2,则直线AC的方程为y=k1x+t,直线BC的方程为y=k2x+t+6.
联立得C点的横坐标为
,
∵|AB|=t+6-t=6,∴S=
|
|×6=|
|
由于圆M与AC相切,所以
=2,∴k1=
同理,k2=
,
∴k1-k2=-
(1+
),
∵-4≤t≤-2,∴-9≤t2+6t≤-8,∴-8≤t2+6t+1≤-4,∴
≤|k1-k2|≤
,
∴Smax=24.
此时t2+6t=-8,t=-2或-4.
22-(
|
| |3a+1| |
| 5 |
又∵M在l的上方,∴3a+1<0,∴-3a-1=5,∴a=-2,故圆的方程为(x+2)2+y2=4;
(2)设AC斜率为k1,BC斜率为k2,则直线AC的方程为y=k1x+t,直线BC的方程为y=k2x+t+6.
联立得C点的横坐标为
| 6 |
| k1-k2 |
∵|AB|=t+6-t=6,∴S=
| 1 |
| 2 |
| 6 |
| k1-k2 |
| 18 |
| k1-k2 |
由于圆M与AC相切,所以
| |-2k1+t| | ||
|
| t2-4 |
| 4t |
同理,k2=
| (t+6)2-4 |
| 4(t+6) |
∴k1-k2=-
| 3 |
| 2 |
| 4 |
| t2+6t |
∵-4≤t≤-2,∴-9≤t2+6t≤-8,∴-8≤t2+6t+1≤-4,∴
| 3 |
| 4 |
| 5 |
| 6 |
∴Smax=24.
此时t2+6t=-8,t=-2或-4.
点评:本题是中档题,考查直线与圆的位置关系,三角形面积的最值的求法,考查计算能力.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
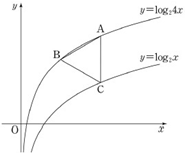 如图所示,已知函数y=log24x图象上的两点A,B和函数y=log2x上的点 C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为(p,q),则实数p的值为
如图所示,已知函数y=log24x图象上的两点A,B和函数y=log2x上的点 C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为(p,q),则实数p的值为