题目内容
下列命题中,真命题是( )
| A、?x0∈R,2 x0≤0 | ||
| B、?x∈R,2x>x2 | ||
C、a+b=0的充要条件是
| ||
| D、a>2,b>2是ab>4的充分条件 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.利用指数函数的性质,?x0∈R,2 x0>0,可判断A;
B.举例24=42=16,可判断B;
C.当b=0时,
无意义,可判断C;
D.利用充分必要条件的概念,可判断D.
B.举例24=42=16,可判断B;
C.当b=0时,
| a |
| b |
D.利用充分必要条件的概念,可判断D.
解答:
解:对于A,?x0∈R,2 x0>0,故A错误;
对于B,由于24=42=16,故?x∈R,2x>x2错,即B错误;
对于C,当b≠0时,a+b=0的充要条件是
=-1,故C错误;
对于D,a>2,b>2⇒ab>4,充分性成立,反之,若ab>4,如(-2)(-3)=6>4,但不满足a>2,b>2,即必要性不成立,故a>2,b>2是ab>4的充分条件,故D正确.
故选:D.
对于B,由于24=42=16,故?x∈R,2x>x2错,即B错误;
对于C,当b≠0时,a+b=0的充要条件是
| a |
| b |
对于D,a>2,b>2⇒ab>4,充分性成立,反之,若ab>4,如(-2)(-3)=6>4,但不满足a>2,b>2,即必要性不成立,故a>2,b>2是ab>4的充分条件,故D正确.
故选:D.
点评:本题考查命题的真假判断与应用,着重考查全称命题与特称命题的关系及真假判断与充分必要条件的概念及应用,属于中档题.

练习册系列答案
相关题目
不等式组
表示的平面区域是( )
|
A、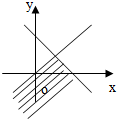 |
B、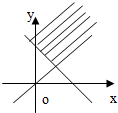 |
C、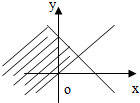 |
D、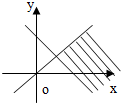 |
函数y=1+4cosx-4sin2x(-
≤x≤
)的值域是( )
| 2π |
| 3 |
| 2π |
| 3 |
| A、[0,8] | ||
| B、[-3,5] | ||
C、[-3,2
| ||
| D、[-4,5] |
设f(x)是奇函数且在(-∞,0)上是减函数,f(-1)=0则不等式xf(x)<0的解集为( )
| A、(-∞,-1)∪(1,+∞) |
| B、(-1,0)∪(0,1) |
| C、(-1,0)∪(1,+∞) |
| D、(-∞,-1)∪(0,1) |
如图,已知正方体ABCD-A1B1C1D1中,异面直线AD1与A1C所成的角的大小是( )


| A、30° | B、60° |
| C、90° | D、120° |
下列四个命题中,为真命题的是( )
| A、若a>b,则ac2>bc2 | ||||
| B、若a>b,c>d则a-c>b-d | ||||
| C、若a>|b|,则a2>b2 | ||||
D、若a>b,则
|
下列求导运算正确的是( )
| A、(cosx)′=sinx | ||||||||
B、(sin
| ||||||||
C、(
| ||||||||
D、(-
|