题目内容
下列四个命题中,为真命题的是( )
| A、若a>b,则ac2>bc2 | ||||
| B、若a>b,c>d则a-c>b-d | ||||
| C、若a>|b|,则a2>b2 | ||||
D、若a>b,则
|
考点:命题的真假判断与应用
专题:不等式的解法及应用
分析:A,若a>b,当c=0时,ac2=bc2,可判断A;
B,令a=3,b=2,c=2,d=0,可判断B;
C,利用不等式的性质可判断C;
D,令a=2>-1=b,可判断D.
B,令a=3,b=2,c=2,d=0,可判断B;
C,利用不等式的性质可判断C;
D,令a=2>-1=b,可判断D.
解答:
解:A,若a>b,当c=0时,ac2=bc2,A错误;
B,若a=3,b=2,c=2,d=0,满足a>b,c>d,但a-c=1<b-d=2,故B错误;
C,若a>|b|,则a2>|b|2=b2,正确;
D,若a=2>-1=b,则
>-1,故
<
错误.
故选:C.
B,若a=3,b=2,c=2,d=0,满足a>b,c>d,但a-c=1<b-d=2,故B错误;
C,若a>|b|,则a2>|b|2=b2,正确;
D,若a=2>-1=b,则
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| b |
故选:C.
点评:本题考查不等式的基本性质及应用,特值法是解决选择题的良好方法,属于中档题.

练习册系列答案
相关题目
下列命题中,真命题是( )
| A、?x0∈R,2 x0≤0 | ||
| B、?x∈R,2x>x2 | ||
C、a+b=0的充要条件是
| ||
| D、a>2,b>2是ab>4的充分条件 |
椭圆3x2+ky2=1的一个焦点的坐标为(0,1),则其离心率为( )
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
已知点A(-1,0),B(1,0),P是平面内一动点,直线PA,PB斜率之积为-
,则动点P的轨迹方程为( )
| 1 |
| 2 |
| A、2x2+y2=1(x≠±1) |
| B、x2+2y2=1(x≠±1) |
| C、x2-2y2=1(x≠±1) |
| D、2x2-y2=1(x≠±1) |
 为庆祝国庆,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(成绩均为整数)分成六段[40,50),[50,60),…,[90,100)后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题:
为庆祝国庆,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(成绩均为整数)分成六段[40,50),[50,60),…,[90,100)后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题: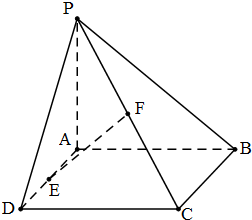 在四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD为矩形,PA=AB,E、F分别为AD、PC的中点,
在四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD为矩形,PA=AB,E、F分别为AD、PC的中点,