题目内容
设f(x)是奇函数且在(-∞,0)上是减函数,f(-1)=0则不等式xf(x)<0的解集为( )
| A、(-∞,-1)∪(1,+∞) |
| B、(-1,0)∪(0,1) |
| C、(-1,0)∪(1,+∞) |
| D、(-∞,-1)∪(0,1) |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:本题可以利用f(x)在(-∞,0)上是减函数,f(-1)=0,得到函数有y轴左侧的图象草图,得到f(x)的相应函数值的正负情况,再根据f(x)是奇函数,得到函数有y轴右侧的图象草图,得到f(x)的相应函数值的正负情况,通过分类讨论,将不等式xf(x)<0转化为不等式组,解不等式组,得到本题结论.
解答:
解:∵f(x)在(-∞,0)上是减函数,f(-1)=0,
∴当x<-1时,f(x)>0;
当-1<x<0时,f(x)<0.
又∵f(x)是奇函数,
∴由图象的对称性知:
当0<x<1时,f(x)>0;
当x>1时,f(x)<0.
若f(0)有意义,则f(0)=0.
∵不等式xf(x)<0,
∴
或
,
∴x>1或x<-1.
故选A.
∴当x<-1时,f(x)>0;
当-1<x<0时,f(x)<0.
又∵f(x)是奇函数,
∴由图象的对称性知:
当0<x<1时,f(x)>0;
当x>1时,f(x)<0.
若f(0)有意义,则f(0)=0.
∵不等式xf(x)<0,
∴
|
|
∴x>1或x<-1.
故选A.
点评:本题考查了函数的单调性与对称性,函数性质与图象间关系,本题难度不大,属于基础题.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
在正方体ABCD-A1B1C1D1中,M是线段A1C1上的动点,则异面直线BM与AB1所成的角的取值范围是( )
A、[
| ||||
B、[
| ||||
C、(
| ||||
D、(
|
下列命题中,真命题是( )
| A、?x0∈R,2 x0≤0 | ||
| B、?x∈R,2x>x2 | ||
C、a+b=0的充要条件是
| ||
| D、a>2,b>2是ab>4的充分条件 |
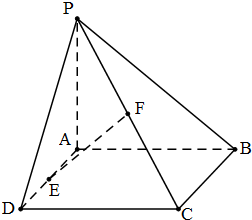 在四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD为矩形,PA=AB,E、F分别为AD、PC的中点,
在四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD为矩形,PA=AB,E、F分别为AD、PC的中点,