题目内容
已知椭圆的中心在坐标原点,焦点在x轴上,离心率为
,且过点(1,2
),求椭圆的标准方程.
| ||
| 2 |
| 3 |
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:先假设椭圆的方程,再利用的椭圆C的离心率为
,且过点(1,2
),即可求得椭圆C的方程.
| ||
| 2 |
| 3 |
解答:
解:设椭圆方程为
+
=1,椭圆的半焦距为c,
∵椭圆C的离心率为
,
∴
=
,∴
=
,①
∵椭圆过点(1,2
),
∴
+
=1②
由①②解得:b2=
,a2=49
∴椭圆C的方程为
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆C的离心率为
| ||
| 2 |
∴
| c |
| a |
| ||
| 2 |
| a2-b2 |
| a2 |
| 3 |
| 4 |
∵椭圆过点(1,2
| 3 |
∴
| 1 |
| a2 |
| 12 |
| b2 |
由①②解得:b2=
| 49 |
| 4 |
∴椭圆C的方程为
| x2 |
| 49 |
| 4y2 |
| 49 |
点评:本题重点考查椭圆的标准方程,考查椭圆的性质,解题的关键是待定系数法.

练习册系列答案
相关题目
等腰三角形ABC底边两端点是A(-
,0),B(
,0),顶点C的轨迹是( )
| 3 |
| 3 |
| A、一条直线 | B、一条直线去掉一点 |
| C、一个点 | D、两个点 |
下列命题中,真命题是( )
| A、?x0∈R,2 x0≤0 | ||
| B、?x∈R,2x>x2 | ||
C、a+b=0的充要条件是
| ||
| D、a>2,b>2是ab>4的充分条件 |
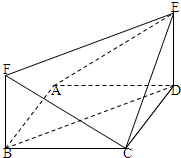 如图,四边形ABCD为正方形,四边形BDEF为矩形,AB=2BF,DE⊥平面ABCD.
如图,四边形ABCD为正方形,四边形BDEF为矩形,AB=2BF,DE⊥平面ABCD. 为庆祝国庆,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(成绩均为整数)分成六段[40,50),[50,60),…,[90,100)后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题:
为庆祝国庆,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(成绩均为整数)分成六段[40,50),[50,60),…,[90,100)后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题: