题目内容
如图,已知正方体ABCD-A1B1C1D1中,异面直线AD1与A1C所成的角的大小是( )


| A、30° | B、60° |
| C、90° | D、120° |
考点:异面直线及其所成的角
专题:空间角
分析:在正方体ABCD-A1B1C1D1中,推出AD1⊥平面A1DC,由此能求出结果.
解答:
 解:如图,在正方体ABCD-A1B1C1D1中,
解:如图,在正方体ABCD-A1B1C1D1中,
连结A1D,A1D⊥DC,A1D⊥AD1,
∴AD1⊥平面A1DC,
∴异面直线AD1与A1C所成的角的大小是90°.
故选:C.
 解:如图,在正方体ABCD-A1B1C1D1中,
解:如图,在正方体ABCD-A1B1C1D1中,连结A1D,A1D⊥DC,A1D⊥AD1,
∴AD1⊥平面A1DC,
∴异面直线AD1与A1C所成的角的大小是90°.
故选:C.
点评:本题考查异面直线所成的角的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
下列命题中,真命题是( )
| A、?x0∈R,2 x0≤0 | ||
| B、?x∈R,2x>x2 | ||
C、a+b=0的充要条件是
| ||
| D、a>2,b>2是ab>4的充分条件 |
已知点A(-1,0),B(1,0),P是平面内一动点,直线PA,PB斜率之积为-
,则动点P的轨迹方程为( )
| 1 |
| 2 |
| A、2x2+y2=1(x≠±1) |
| B、x2+2y2=1(x≠±1) |
| C、x2-2y2=1(x≠±1) |
| D、2x2-y2=1(x≠±1) |
 为庆祝国庆,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(成绩均为整数)分成六段[40,50),[50,60),…,[90,100)后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题:
为庆祝国庆,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(成绩均为整数)分成六段[40,50),[50,60),…,[90,100)后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题: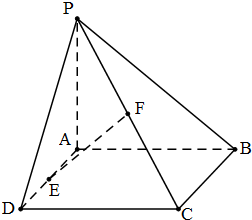 在四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD为矩形,PA=AB,E、F分别为AD、PC的中点,
在四棱锥P-ABCD中,PA⊥面ABCD,底面ABCD为矩形,PA=AB,E、F分别为AD、PC的中点,