题目内容
为丰富广大中学生的课余文化生活,拓展知识面,某市教育局举办了太空天文知识竞赛活动.题目均为选择题,共50题,每答对一题得2分,满分100分,每题的正确答案只有一个,现随机抽取了某中学50名学生本次竞赛的成绩,整理并制成如表:
(Ⅰ)绘制出被抽查的学生成绩的频率分布直方图;
(Ⅱ)若从成绩在[40,50)中随机选出1名学生,从成绩在[90,100]中随机选出2名学生,共3名学生召开座谈会,求[40,50)组中的学生A1和[90,100]组中的学生B1同时被选中的概率.
| 成绩 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100 ] |
| 频数 | 2 | 3 | 14 | 15 | 12 | 4 |
(Ⅱ)若从成绩在[40,50)中随机选出1名学生,从成绩在[90,100]中随机选出2名学生,共3名学生召开座谈会,求[40,50)组中的学生A1和[90,100]组中的学生B1同时被选中的概率.
考点:古典概型及其概率计算公式,频率分布直方图
专题:概率与统计
分析:(Ⅰ)由题意可知各组的概率即图中各组的纵坐标,即可绘制出被抽查的学生成绩的频率分布直方图;
(Ⅱ)分别列举出所有可能的基本事件的个数和所求事件所含的基本事件的个数,用古典概型的概率求法公式即可得解.
(Ⅱ)分别列举出所有可能的基本事件的个数和所求事件所含的基本事件的个数,用古典概型的概率求法公式即可得解.
解答:
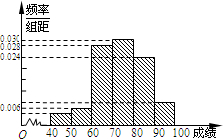 解:(Ⅰ)各组的概率分别为0.04,0.06,0.28,0.30,0.24,0.08,所以图中各组的纵坐标分别为:
解:(Ⅰ)各组的概率分别为0.04,0.06,0.28,0.30,0.24,0.08,所以图中各组的纵坐标分别为:
0.004,0.006,0.028,0.030,0.024,0.008.
(Ⅱ)记[40,50)中的学生为A1、A2,[90,100)中的学生为B1、B2、B3、B4,
由题意可得,基本事件为:A1B1B2,A1B1B3,A1B1B4,A1B2B3,A1B2B4,A1B3B4,
A2B1B2,A2B1B3,A2B1B4,A2B2B3,A2B2B4,A2B3B4共12个
事件“A1B1同时被选中”发生有:A1B1B2,A1B1B3,A1B1B4三个,
所以由古典概型知,P(A)=
=
.
 解:(Ⅰ)各组的概率分别为0.04,0.06,0.28,0.30,0.24,0.08,所以图中各组的纵坐标分别为:
解:(Ⅰ)各组的概率分别为0.04,0.06,0.28,0.30,0.24,0.08,所以图中各组的纵坐标分别为:0.004,0.006,0.028,0.030,0.024,0.008.
(Ⅱ)记[40,50)中的学生为A1、A2,[90,100)中的学生为B1、B2、B3、B4,
由题意可得,基本事件为:A1B1B2,A1B1B3,A1B1B4,A1B2B3,A1B2B4,A1B3B4,
A2B1B2,A2B1B3,A2B1B4,A2B2B3,A2B2B4,A2B3B4共12个
事件“A1B1同时被选中”发生有:A1B1B2,A1B1B3,A1B1B4三个,
所以由古典概型知,P(A)=
| 3 |
| 12 |
| 1 |
| 4 |
点评:本题考查频率分布直方图和古典概型,要求会用频率分布直方图,掌握古典概型的求法,属简单题.

练习册系列答案
相关题目
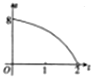
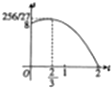
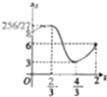
 如图是一块不规则的铁皮,已知AB⊥BC,OA∥BC,AB=PC=2OA=4,曲线段OC是以点O为顶点,且开口向右的抛物线的一段,现用这块铁皮截出一块矩形铁皮,其中矩形的一对邻边分别在AB、BC上,且一个顶点P落在曲线段OC上,设点P到直线AB的距离为t+2,所截矩形铁皮的面积为S,则函数S=f(t)的图象大致是( )
如图是一块不规则的铁皮,已知AB⊥BC,OA∥BC,AB=PC=2OA=4,曲线段OC是以点O为顶点,且开口向右的抛物线的一段,现用这块铁皮截出一块矩形铁皮,其中矩形的一对邻边分别在AB、BC上,且一个顶点P落在曲线段OC上,设点P到直线AB的距离为t+2,所截矩形铁皮的面积为S,则函数S=f(t)的图象大致是( )