题目内容
在△ABC中,∠ACB=60°,∠ABC=θ,AB=6
(1)求△ABC面积的最大值.
(2)若△ABC的周长为6
+6,求θ的值.
(1)求△ABC面积的最大值.
(2)若△ABC的周长为6
| 3 |
考点:余弦定理,正弦定理
专题:三角函数的求值
分析:(1)利用余弦定理列出关系式,将cos∠ACB与c的值代入,利用基本不等式变形求出ab的最大值,最后利用三角形面积公式即可求出三角形ABC面积的最大值;
(2)在三角形ABC中,利用正弦定理列出关系式,表示出b与a的值,进而表示出三角形周长,整理后即可求出θ的度数.
(2)在三角形ABC中,利用正弦定理列出关系式,表示出b与a的值,进而表示出三角形周长,整理后即可求出θ的度数.
解答:
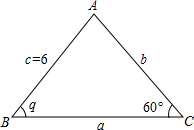 解:(1)∵c=6,cos∠ACB=cos60°,
解:(1)∵c=6,cos∠ACB=cos60°,
∴由余弦定理得:36=c2=a2+b2-2abcos60°=a2+b2-ab≥2ab-ab=ab,
即ab≤36,
∴S=
absin60°≤9
,
则S的最大值为9
;
(2)在△ABC中,利用正弦定理得:
=
=
,
∴b=4
sinq,a=4
sin(120°-q),
∴三角形周长为6
+6=a+b+c=4
sinq+4
sin(120°-q)+6,
整理得:sinq+sin(120°-q)=
,即sin(q+30°)=
,
∴q+30°=60°或q+30°=120°,
则θ=q=30°或90°.
 解:(1)∵c=6,cos∠ACB=cos60°,
解:(1)∵c=6,cos∠ACB=cos60°,∴由余弦定理得:36=c2=a2+b2-2abcos60°=a2+b2-ab≥2ab-ab=ab,
即ab≤36,
∴S=
| 1 |
| 2 |
| 3 |
则S的最大值为9
| 3 |
(2)在△ABC中,利用正弦定理得:
| 6 |
| sin60° |
| b |
| sinq |
| a |
| sin(120°-q) |
∴b=4
| 3 |
| 3 |
∴三角形周长为6
| 3 |
| 3 |
| 3 |
整理得:sinq+sin(120°-q)=
| 3 |
| 2 |
| ||
| 2 |
∴q+30°=60°或q+30°=120°,
则θ=q=30°或90°.
点评:此题考查了正弦、余弦定理,以及基本不等式的运用,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
P为函数y=ex图象上的点,则点P到直线y=x的最短距离为( )
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|