题目内容
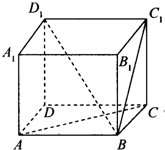 在正方体ABCD-A1B1C1D1中,解答下列问题:
在正方体ABCD-A1B1C1D1中,解答下列问题:(1)指出直线AB与CC1的位置关系;
(2)求直线AD与BC1所成角的大小;
(3)证明BD1⊥AC.
考点:异面直线及其所成的角,直线与平面垂直的性质
专题:计算题,证明题,空间位置关系与距离
分析:(1)由异面直线的判定,即可得到;(2)由于BC∥AD,则∠CBC1即为直线AD与BC1所成角,求出即可得到;(3)由线面垂直的性质和判定定理,即可得证.
解答:
 (1)解:由于AB?平面ABCD,C∉AB,C1∉平面ABCD,
(1)解:由于AB?平面ABCD,C∉AB,C1∉平面ABCD,
则由异面直线的判定,即可得到,直线AB与CC1是异面直线;
(2)解:由于BC∥AD,则∠CBC1即为直线AD与BC1所成角,
由于正方形BCC1B1,即有∠CBC1=45°,
则直线AD与BC1所成角为45°;
(3)证明:连接BD,则正方形ABCD中,AC⊥BD,
又DD1⊥平面ABCD,则DD1⊥AC,
则AC⊥平面BDD1,即有AC⊥BD1.
 (1)解:由于AB?平面ABCD,C∉AB,C1∉平面ABCD,
(1)解:由于AB?平面ABCD,C∉AB,C1∉平面ABCD,则由异面直线的判定,即可得到,直线AB与CC1是异面直线;
(2)解:由于BC∥AD,则∠CBC1即为直线AD与BC1所成角,
由于正方形BCC1B1,即有∠CBC1=45°,
则直线AD与BC1所成角为45°;
(3)证明:连接BD,则正方形ABCD中,AC⊥BD,
又DD1⊥平面ABCD,则DD1⊥AC,
则AC⊥平面BDD1,即有AC⊥BD1.
点评:本题考查空间直线和直线的位置关系,考查空间异面直线所成角的求法和线面垂直的判定和性质及运用,属于基础题.

练习册系列答案
相关题目
| ∫ |
0 |
| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
已知数列{an}的前n项和为Sn=kn2,若对所有的n∈N*,都有an+1>an,则实数k的取值范围是( )
| A、k<0 | B、k<1 |
| C、k>1 | D、k>0 |
抛物线y2=4x上一点M与该抛物线的焦点F的距离|MF|=4,则点M的横坐标x=( )
| A、2 | B、3 | C、4 | D、5 |
已知函数y=-sin
x在区间[0,t]上至少取得2个最大值,则正整数t的最小值是( )
| π |
| 3 |
| A、9 | B、10 | C、11 | D、12 |