题目内容
已知函数y=-sin
x在区间[0,t]上至少取得2个最大值,则正整数t的最小值是( )
| π |
| 3 |
| A、9 | B、10 | C、11 | D、12 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:根据函数的图象结合在区间[O,t]上至少取得2个最大值,得到函数区间满足的条件即可得到结论.
解答:
 解:∵y=-sin
解:∵y=-sin
x,
∴函数的周期T=
=6,
要使y=-sin
x在区间[O,t]上至少取得2个最大值,
则t≥T+
即可,
即t≥6+4
,
∵t为正整数,
∴t≥11.
即正整数t的最小值是11.
选:C.
 解:∵y=-sin
解:∵y=-sin| π |
| 3 |
∴函数的周期T=
| 2π | ||
|
要使y=-sin
| π |
| 3 |
则t≥T+
| 3T |
| 4 |
即t≥6+4
| 1 |
| 2 |
∵t为正整数,
∴t≥11.
即正整数t的最小值是11.
选:C.
点评:本题主要考查三角函数的图象和性质,利用数形结合是解决本题的关键,属于基本知识的考查.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
下列各小题中,p是q的充分必要条件的是( )
①p:m<-2,或m>6;q:x2+mx+m+3有两个不同的零点;
②p:
=1;q:y=f(x)是偶函数;
③p:cosα=cosβ;q:tanα=tanβ;
④p:A∩B=A;q:∁UB⊆∁UA.
①p:m<-2,或m>6;q:x2+mx+m+3有两个不同的零点;
②p:
| f(-x) |
| f(x) |
③p:cosα=cosβ;q:tanα=tanβ;
④p:A∩B=A;q:∁UB⊆∁UA.
| A、①② | B、②③ | C、③④ | D、①④ |
某厂的产值若每年平均比上一年增长10%,经过x年后,可以增长到原来的2倍,在求x时,所列的方程正确的是( )
| A、(1+10%)x-1=2 |
| B、(1+10%)x=2 |
| C、(1+10%)x+1=2 |
| D、x=(1+10%)2 |
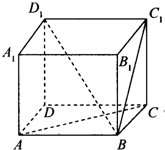 在正方体ABCD-A1B1C1D1中,解答下列问题:
在正方体ABCD-A1B1C1D1中,解答下列问题: