题目内容
已知
=（cosθ，sinθ），
=（
，-1），则|2
-
|的最大值为 ．
| a |
| b |
| 3 |
| a |
| b |
考点：平面向量数量积的运算
专题：三角函数的求值,平面向量及应用
分析：运用向量的模的公式和数量积的坐标表示，求出向量a，b的模和数量积，化简整理，即可得到最大值．
解答：
解：∵
=（cosθ，sinθ），
=（
，-1），
∴|
|=1，|
|=2，
•
=
cosθ-sinθ=2sin（
-θ），
∴|2
-
|2=4|
|2+|
|2-4
•
=4×1+4-4×2sin（
-θ）=8-8sin（
-θ），
∵-1≤sin（
-θ）≤1，
∴sin（
-θ）=-1时，有最大值，即|2
-
|2=16，
∴|2
-
|=4，
∴|2
-
|的最大值为4，
故答案为：4
| a |
| b |
| 3 |
∴|
| a |
| b |
| a |
| b |
| 3 |
| π |
| 3 |
∴|2
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 3 |
| π |
| 3 |
∵-1≤sin（
| π |
| 3 |
∴sin（
| π |
| 3 |
| a |
| b |
∴|2
| a |
| b |
∴|2
| a |
| b |
故答案为：4
点评：本题考查平面向量的数量积的坐标表示和性质：向量的平方即为模的平方，同时考查三角函数的化简和求值，注意运用两角差的正弦公式，属于中档题
练习册系列答案
相关题目
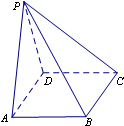如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，且PA=PD=
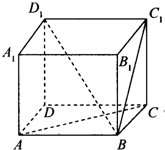在正方体ABCD-A1B1C1D1中，解答下列问题：