题目内容
如图,已知正方形ABCD的边长为2,AC∩BD=O.将正方形ABCD沿对角线BD折起,得到三棱锥A-BCD.
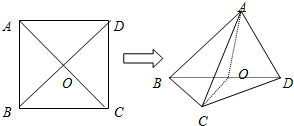
(1)求证:面AOC⊥面BCD;
(2)若∠AOC=60°,求三棱锥A-BCD的体积.

(1)求证:面AOC⊥面BCD;
(2)若∠AOC=60°,求三棱锥A-BCD的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)运用直线与平面,平面与平面的垂直问题求解判断.(2)转化VA-BCD=2VD-ACO,运用体积公式求解即可.
解答:
解:(1)证明:因为AC、BD是正方形
ABCD的对角线,所以AC⊥BD.
故在折叠后的△ABD和△BCD中,有
BD⊥AO,BD⊥CO.
又AO∩CO=O,所以BD⊥平面AOC.
因为BD?平面BCD,所以平面AOC⊥
平面BCD.
(2)∵BD⊥AO,BD⊥CO.
又AO∩CO=O,所以BD⊥平面AOC.
∵∠AOC=60°,正方形ABCD的边长为2
∴S△ACO=
×(
)2=
,OD=
,
∴VA-BCD=2VD-ACO=2×
×
×
=
,
故棱锥A-BCD的体积为:
.
ABCD的对角线,所以AC⊥BD.
故在折叠后的△ABD和△BCD中,有
BD⊥AO,BD⊥CO.
又AO∩CO=O,所以BD⊥平面AOC.
因为BD?平面BCD,所以平面AOC⊥
平面BCD.
(2)∵BD⊥AO,BD⊥CO.
又AO∩CO=O,所以BD⊥平面AOC.
∵∠AOC=60°,正方形ABCD的边长为2
∴S△ACO=
| ||
| 4 |
| 2 |
| ||
| 2 |
| 2 |
∴VA-BCD=2VD-ACO=2×
| 1 |
| 3 |
| ||
| 2 |
| 2 |
| ||
| 3 |
故棱锥A-BCD的体积为:
| ||
| 3 |
点评:本题考查了平面图形的折叠问题,空间几何题的体积面积问题,属于中档题.

练习册系列答案
相关题目
为了得到函数y=cos(2x-
)的图象,可以将函数y=-sin2x的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
 在正方体ABCD-A1B1C1D1中,解答下列问题:
在正方体ABCD-A1B1C1D1中,解答下列问题: