题目内容
已知数列{an}的前n项和为Sn=kn2,若对所有的n∈N*,都有an+1>an,则实数k的取值范围是( )
| A、k<0 | B、k<1 |
| C、k>1 | D、k>0 |
考点:数列的求和
专题:等差数列与等比数列
分析:由Sn=kn2,可得an+1=Sn+1-Sn=(2n+1)k.利用对所有的n∈N*,都有an+1>an,即可得出.
解答:
解:∵Sn=kn2,∴an+1=Sn+1-Sn=k(n+1)2-kn2=(2n+1)k.
∵对所有的n∈N*,都有an+1>an,
∴(2n+1)k>(2n-1)k,
化为k>0,
故选:D.
∵对所有的n∈N*,都有an+1>an,
∴(2n+1)k>(2n-1)k,
化为k>0,
故选:D.
点评:本题考查了递推式的意义、数列的单调性,属于基础题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
为了得到函数y=cos(2x-
)的图象,可以将函数y=-sin2x的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
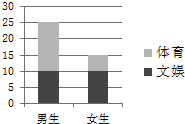 对某班学生是更喜欢体育还是更喜欢文娱进行调查,根据调查得到的数据,所绘制的二维条形图如图.
对某班学生是更喜欢体育还是更喜欢文娱进行调查,根据调查得到的数据,所绘制的二维条形图如图.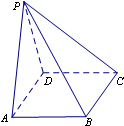 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=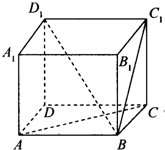 在正方体ABCD-A1B1C1D1中,解答下列问题:
在正方体ABCD-A1B1C1D1中,解答下列问题: