题目内容
抛物线y2=4x上一点M与该抛物线的焦点F的距离|MF|=4，则点M的横坐标x=（ ）
| A、2 | B、3 | C、4 | D、5 |
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由抛物线定义可知，抛物线上任一点到焦点的距离与到准线的距离是相等的，已知|MF|=4，则M到准线的距离也为4，即点M的横坐标x+
=4，将p的值代入，进而求出x．
| p |
| 2 |
解答：
解：∵抛物线y2=4x=2px，
∴p=2，
由抛物线定义可知，抛物线上任一点到焦点的距离与到准线的距离是相等的，
∴|MF|=4，即有x+
=4，
∴x=3，
故选B．
∴p=2，
由抛物线定义可知，抛物线上任一点到焦点的距离与到准线的距离是相等的，
∴|MF|=4，即有x+
| p |
| 2 |
∴x=3，
故选B．
点评：活用抛物线的定义是解决抛物线问题最基本的方法．抛物线上的点到焦点的距离，叫焦半径．到焦点的距离常转化为到准线的距离求解．
练习册系列答案
相关题目
为了得到函数y=cos（2x-
）的图象，可以将函数y=-sin2x的图象（ ）
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
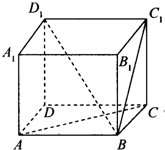在正方体ABCD-A1B1C1D1中，解答下列问题：